Esta revisión establece una guía práctica que comprende los conceptos básicos de los análisis de supervivencia y su aplicación en el estudio de las enfermedades cardiovasculares, si bien gran parte del contenido puede extrapolarse a otras ramas de la medicina. Este es el primero de dos artículos académicos que sientan las bases para abordar las principales cuestiones metodológicas empleadas en estudios de supervivencia, y guían al lector desde los análisis más básicos hasta los más complejos. Esta revisión se centra en el tipo y la forma de los datos de supervivencia, así como en los métodos estadísticos más utilizados, como las pruebas no paramétricas, paramétricas y semiparamétricas. La interpretación y la valoración de la idoneidad de dichos métodos, así como sus ventajas e inconvenientes, se ilustran con estudios del ámbito de las enfermedades cardiovasculares. El artículo concluye aportando un conjunto de recomendaciones para guiar la estrategia del análisis de supervivencia, tanto en el contexto de un ensayo clínico aleatorizado como en el de estudios observacionales. En la segunda revisión se abordarán temas como el modelo de riesgos competitivos, el modelo de eventos recurrentes y los modelos multiestado.
Palabras clave
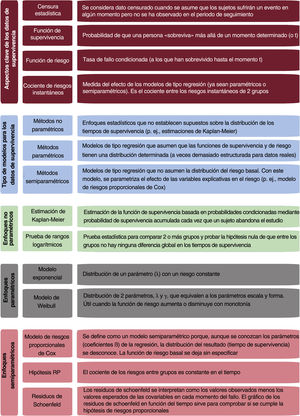
El presente artículo ofrece una visión general del análisis de supervivencia en la investigación cardiovascular y tiene por objetivo proporcionar una herramienta práctica para comprender la variedad de enfoques estadísticos para abordar los resultados observados durante el tiempo transcurrido hasta el evento. Se describen de forma resumida las características de los datos supervivencia y se ofrece una visión general de varios enfoques analíticos. Para una mejor comprensión, se ilustra cómo se han aplicado estos métodos a los datos de supervivencia de los estudios cardiovasculares. El contenido de esta revisión es principalmente descriptivo y, por lo tanto, no es necesario tener conocimientos matemáticos o estadísticos previos. Los conceptos básicos se resumen en la figura 1.
Los análisis de supervivencia se aplican cuando la medida de interés es el tiempo transcurrido hasta que tiene lugar un evento (resultados observados durante el tiempo transcurrido hasta el evento). Pese a utilizarse la palabra «supervivencia», el evento o resultado puede ser mortal o no mortal (p. ej., mortalidad cardiovascular o infarto de miocardio)1. Para referirse al momento en que tiene lugar el evento, se habla de tiempo hasta el evento o tiempo de supervivencia. El primero de estos términos surge de los métodos estadísticos creados para el análisis de datos en los ensayos sobre cáncer y el segundo, del control de calidad en el entorno industrial. A pesar de la expresión, el evento en estudio no es necesariamente un fallo con connotaciones negativas, es decir, podría tratarse de un evento positivo, como la descarga apropiada de un desfibrilador automático implantable2.
El tiempo de supervivencia de cada sujeto es el transcurrido desde el momento inicial hasta que tiene lugar el evento de interés1,3. En un ensayo clínico aleatorizado (ECA), el tiempo de supervivencia suele estimarse a partir de la aleatorización (normalmente al comienzo de la intervención)4. En un estudio observacional, el tiempo de supervivencia se calcula a partir del momento de inclusión en el estudio, desde una fecha concreta, como aquella en que los participantes se exponen por primera vez a un factor de riesgo (p. ej., quimioterapia) o a un evento índice (p. ej., síndrome coronario agudo [SCA])5. A veces también se calcula a partir de un punto de corte de edad.
Fuentes de los datos de supervivenciaHay 2 fuentes principales de los datos de supervivencia en la investigación cardiovascular: los ECA y los estudios observacionales.
En los ECA, el objetivo suele ser dar pruebas fiables de la eficacia del tratamiento (o la eficacia en condiciones reales) y la seguridad. El ejemplo más sencillo se refiere a los sujetos que cumplen los criterios de inclusión en el estudio, son aleatorizados a la intervención o al grupo de control y se someten a seguimiento durante un tiempo determinado para recabar información sobre los eventos y el tiempo transcurrido hasta que tienen lugar. Por ejemplo, el ensayo REBOOT (NCT03596385) asigna aleatoriamente a los pacientes que sufren un infarto de miocardio agudo con fracción de eyección del ventrículo izquierdo ≥ 40% a un tratamiento habitual con o sin bloqueadores beta y les da seguimiento durante una media de 2,75 años para evaluar diferencias en la incidencia del objetivo compuesto mortalidad por cualquier causa, reinfarto no mortal u hospitalización por insuficiencia cardiaca.
En los estudios observacionales prospectivos (estudios de cohortes), se incluye a los sujetos que difieren en 1 factor de la exposición primaria en una cohorte y se los sigue durante distintos periodos de tiempo, para comparar los resultados observados durante el tiempo transcurrido hasta el evento entre los sujetos expuestos y los no expuestos al factor6. El registro EPICOR (Long-term follow up of antithrombotic management patterns in acute coronary syndrome patients) es un estudio de cohortes internacional que incluye a pacientes dados de alta tras un SCA a los que se siguió durante 2 años por distintos eventos7. El momento en que iniciaron el estudio (momento cero) se determinó en el momento del alta del evento índice (SCA), y los eventos recabados durante el seguimiento fueron otros eventos cardiovasculares (como un SCA recurrente) y eventos fatales. El registro EPICOR se ha utilizado para evaluar diferencias en la mortalidad por cualquier causa en distintas exposiciones, tales como el origen geográfico de los participantes8,9 o si se han sometido a revascularización coronaria5.
Además de los ECA y los estudios observacionales, otras fuentes de datos de supervivencia son los registros de datos administrativos. En España, se ha utilizado el Conjunto Mínimo Básico de Datos para explicar las tendencias temporales y las complicaciones hospitalarias de varias enfermedades cardiovasculares10. No obstante, su naturaleza transversal hace imposible cualquier análisis del tiempo transcurrido hasta el evento.
Características de los datos de supervivencia: censura estadística no informativaUn problema analítico clave en los estudios longitudinales (tanto los ECA como los observacionales) es que el tiempo transcurrido hasta el evento de interés puede censurarse, es decir, que el seguimiento de algunos participantes no es completo y por ello no se observa si ocurre el evento. En general hay 3 motivos para censurar durante el periodo de estudio de un ECA concreto que evalúa la presencia de eventos cardiovasculares adversos mayores (MACE): a) los pacientes que siguen vivos al final del seguimiento no han registrado el evento; b) a partir de una fecha concreta del seguimiento se han perdido participantes (p. ej., migración), y c) hay pacientes que fallecieron por una causa distinta (p. ej., cáncer). En cualquiera de estas situaciones, se desconoce el tiempo de supervivencia real (p. ej., tiempo transcurrido hasta un MACE). No sería conveniente excluir de los análisis a tales sujetos, porque el hecho de que no sufrieran MACE mientras formaban parte del estudio ya da cierta información sobre la supervivencia. Hay que tener en cuenta que solo se observa hasta un momento en que se sabe que estos sujetos no sufrieron evento alguno a «la derecha» del periodo de seguimiento (fenómeno que se conoce como «censura estadística por la derecha»)1.
El concepto de «datos censurados» es lo que hace que los análisis de supervivencia sean únicos. Se dispone de 2 tipos de datos de cada paciente: a) un tiempo que corresponde al transcurrido hasta que tiene lugar el evento, o tiempo durante el cual se siguió al paciente, y b) un indicador que denota si el tiempo es tiempo hasta el evento o tiempo hasta ser censurado. Para cada paciente hay un tiempo transcurrido hasta el evento o un tiempo hasta ser censurado tras la cual dejará de seguirse al paciente. A lo largo de esta revisión se asume que un evento censurado no es informativo sobre el tiempo transcurrido hasta el evento1. Esto quiere decir que el momento en que un sujeto es censurado o el hecho de que sea objeto de censura no tienen relación alguna con el resultado del tiempo transcurrido hasta el evento. Si un paciente incluido en un ECA abandona el estudio por razones relacionadas con el estudio (p. ej., participantes en el grupo de la intervención que se sienten mejor o que sufren efectos adversos), el dato censurado es informativo.
Transgredir esta presunción estadística cuestiona los principios de las principales estrategias aplicadas a los datos de supervivencia11. Los métodos para tratar los datos censurados debido a un evento competitivo (p. ej., mortalidad por otra causa) se discutirán en la siguiente revisión.
Conceptos clave en la distribución de datos de supervivenciaSe requieren 2 funciones relevantes para comprender y explicar las distribuciones de supervivencia. La función de supervivencia S(t) se define como la probabilidad de que una persona «sobreviva» más allá de cualquier tiempo (t) especificado, mientras que la función de riesgo r(t) se define como la probabilidad de que le suceda el evento en ese instante. La función de riesgo es una probabilidad de aparición del evento condicional (condicionada a aquellos que han sobrevivido hasta el tiempo t). Por ejemplo, en un estudio que evalúa MACE, la función de supervivencia en el segundo año solo se aplica a quienes no sufrieron evento alguno durante este segundo año y no tiene en cuenta a los que sufrieron MACE con anterioridad. Hay que tener en cuenta que, a diferencia de la función de supervivencia que se centra en la ausencia del evento, la función de riesgo se centra en la aparición del evento.
El cociente de riesgos instantáneos (hazard ratio [HR]) es una medida de efecto y asociación que se utiliza mucho en los análisis de supervivencia. En su forma más simple, el HR puede interpretarse como la probabilidad de que un evento ocurra en el grupo de tratamiento (o grupo expuesto) dividida por la probabilidad de que el evento ocurra en el grupo de control (o grupo no expuesto) de un ECA (o un estudio observacional). El HR resume la relación entre los riesgos instantáneos (o tasas de eventos) en los 2 grupos. El HR se calcula con los análisis de regresión.
Objetivos y estrategias de los análisis de supervivenciaLa mayor parte de los estudios clínicos hacen hincapié en evaluar el impacto de una intervención (p. ej., bloqueadores beta) o exposición (p. ej., origen geográfico) en un resultado de interés (p. ej., MACE). En el contexto de los análisis de supervivencia, el resultado de interés es el tiempo de supervivencia, y el objetivo es comparar los tiempos de supervivencia entre los grupos de tratamiento o evaluar la relación entre los tiempos de supervivencia de los participantes expuestos frente a los no expuestos.
Los métodos para analizar los datos de supervivencia deben tener en cuenta los datos censurados y que los tiempos de supervivencia son exclusivamente no negativos y suelen presentar censura por la derecha. Si se excluyeran del análisis las observaciones que han sido objeto de censura, los resultados estarían sesgados y las estimaciones no serían fiables. En esta revisión se presentan 3 enfoques básicos:
Métodos no paramétricos. Estos métodos relativamente simples (p. ej., método de Kaplan-Meier) no establecen supuestos sobre la distribución de los tiempos de supervivencia. Son excelentes para los análisis univariantes (p. ej., resultado principal en los ECA), pero no suficientes para tratar problemas más complejos, como los factores de confusión en los estudios observacionales.
Métodos totalmente paramétricos. Son análisis de regresión para datos de supervivencia (p. ej., modelo de Weibull), que son análogos a los métodos de regresión para otros tipos de respuesta (p. ej., regresión lineal para datos continuos o regresión logística para una respuesta binaria). Sin embargo, se basan en supuestos sobre el patrón de los tiempos de supervivencia que requieren una evaluación minuciosa.
Métodos semiparamétricos. Llevan a otro tipo de análisis de regresión para datos de supervivencia, lo que a menudo se denomina regresión de Cox. Se parametriza el modo en que los tiempos de supervivencia se relacionan con las exposiciones de interés, si bien se deja sin especificar parte de la distribución total de los tiempos de supervivencia.
ANÁLISIS NO PARAMÉTRICO DE LOS DATOS DE SUPERVIVENCIALas técnicas no paramétricas no establecen ningún supuesto sobre la distribución de los tiempos de supervivencia, lo que tiene sentido, puesto que los datos de supervivencia tienen una distribución sesgada. El enfoque no paramétrico más habitual para la distribución de la función de supervivencia es el método de Kaplan-Meier. Este método se sirve del evento real observado y de los tiempos de censura estadística.
¿Por qué se utilizan métodos no paramétricos?Los métodos no paramétricos son un buen comienzo en la mayoría de los análisis de supervivencia. En primer lugar, permiten estimar las funciones de supervivencia y de riesgo sin necesidad de establecer supuestos paramétricos. En segundo lugar, son un modo muy intuitivo de mostrar de manera gráfica los datos de supervivencia teniendo en cuenta los datos censurados. En tercer lugar, son técnicas óptimas para comparar el tiempo de supervivencia por grupos de sujetos (variables categóricas). Por último, los métodos no paramétricos sirven para obtener información sobre si alguno de los supuestos del modelo puede aplicarse a enfoques más complejos de datos de supervivencia (p. ej., asunción de riesgos proporcionales).
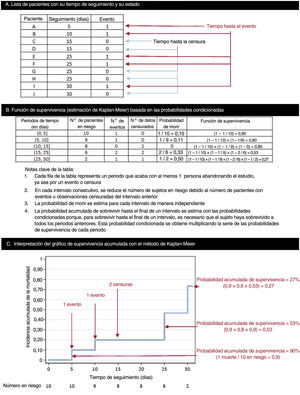
Estimación de la función de supervivencia: método de Kaplan-MeierEl modo más simple de obtener una estimación de la función de supervivencia es calculando la supervivencia acumulada de los participantes incluidos en una cohorte. Esto puede conseguirse con el método de Kaplan-Meier, que estima las probabilidades de la supervivencia acumulada (y del evento) cada vez que un participante abandona el estudio. La estimación de Kaplan-Meier también se conoce como «método del límite de producto». Este enfoque se basa en probabilidades condicionadas y se explica de manera exhaustiva en la figura 2.
Cómo realizar una curva de Kaplan-Meier y estimar su función de supervivencia. A: en este ejemplo, se estableció un conjunto básico de datos de 10 pacientes con un seguimiento a 30 días; para todos ellos existe «el riesgo» de que tenga lugar el evento en el momento 0; 5 pacientes presentan el evento (días 5, 10, 25, 25 y 30), mientras que los otros 5 son censurados: 4 se pierden durante el seguimiento (2 el día 15 y otros 2 el día 25), y solo 1 termina el seguimiento sin que haya ocurrido ningún evento (censurado el día 30). B: estimación de la función de supervivencia con el método de Kaplan-Meier. C: interpretación de las probabilidades de supervivencia acumulada; como en el ejemplo, la estimación de la supervivencia de Kaplan-Meier a veces es un gráfico formado por peldaños, más que una curva uniforme, lo cual refleja que se trata de una estimación empírica de la experiencia de supervivencia de una cohorte en cada instante. Los datos censurados no reducen la supervivencia acumulada, sino que se ajusta el número en riesgo cuando tiene lugar el siguiente evento.
Otro enfoque no paramétrico es el método de la tabla de vida de la función de supervivencia. En el caso de la estimación de Kaplan-Meier, se asume un momento muy concreto (todos los tiempos de supervivencia se observan en un momento exacto). A veces esta información es menos precisa y los tiempos de supervivencia se observan dentro de un intervalo de tiempo. Un ejemplo típico es la evaluación del número de muertes anuales en una población en estudio. En este contexto, el método de la tabla de vida sigue siendo el habitual porque ofrece un resumen sencillo de los datos de supervivencia en poblaciones grandes dentro de intervalos de tiempo12.
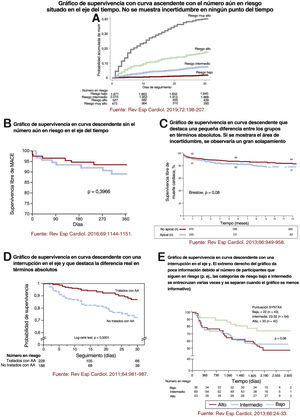
Recomendaciones para representar gráficos de Kaplan-MeierLos gráficos de Kaplan-Meier aparecen en casi todos los artículos que tratan análisis de supervivencia. Por ello es importante dar algunas indicaciones para que su representación sea la adecuada. Una curva de Kaplan-Meier mal trazada puede llevar a que los lectores los malinterpreten. En un artículo de referencia publicado hace unos 20 años, Pocock, Clayton y Altman examinaron los gráficos de supervivencia que aparecían en 35 ECA y dieron algunas recomendaciones importantes que tener en cuenta al presentar gráficos de Kaplan-Meier3. En la mayoría de los casos, los gráficos de supervivencia se presentan mejor en sentido ascendente (proporción acumulada que experimenta el evento) que descendente (proporción acumulada sin eventos). Normalmente, los gráficos ascendentes destacan las diferencias relativas, porque el eje x puede adaptarse a la escala de las curvas. En cambio, los gráficos descendentes (que utilizan todo el eje vertical desde el 0 al 100%) hacen que las diferencias parezcan mucho menos pronunciadas y resaltan básicamente diferencias en términos absolutos. Así pues, debería evitarse una interrupción en el eje y. Pasar por alto una interrupción de este tipo podría llevar al lector a percibir erróneamente el posible efecto terapéutico (o la asociación), que parecería mayor que la diferencia real. En teoría, los gráficos deberían incluir alguna medida de la incertidumbre estadística: el error estándar (o intervalo de confianza del 95% [IC95%]) para poder calcular la proporción estimada de pacientes que han experimentado (o no) el evento en cualquier momento. En los pocos casos en que esta incertidumbre se refleja, hay un aumento de tamaño de la barra que representa el error estándar (o el IC95%) a lo largo del tiempo, lo que ilustra la disminución del número de participantes en riesgo durante el seguimiento. Por último, los gráficos deberían extenderse en el tiempo hasta que el número de participantes en el estudio sea suficiente, y el número de participantes en riesgo que permanecen en el estudio debe mostrarse debajo del eje x. Si el número de participantes disminuye de manera notoria durante el estudio, hay que ser prudentes a la hora de interpretar diferencias entre las curvas del lado derecho del gráfico. Estas recomendaciones se ilustran en la figura 3 con ejemplos de artículos publicados en Revista Española de Cardiología13–17.
A-E: cinco ejemplos que ilustran distintos modos de mostrar curvas de Kaplan-Meier. Reproducido con la autorización de Elsevier y Revista Española de Cardiología. Debajo de cada diagrama de Kaplan-Meier se explicita su fuente y todas las referencias aparecen en «Bibliografía»13–17. AA: antagonista de la aldosterona.
La log-rank test, o prueba de rangos logarítmicos, sirve para comparar las distribuciones de supervivencia de 2 o más grupos. Esta prueba no paramétrica, que solo asume que los datos censurados son no informativos, se basa en una idea muy sencilla: comparar los eventos observados con los esperados en cada grupo. Para comparar 2 grupos (p. ej., comprobar la hipótesis nula, es decir, que la supervivencia es la misma para los pacientes aleatorizados a bloqueadores beta y al grupo control), se calcula el número de eventos esperados en cada grupo con la fórmula habitual para tablas 2 × 2 para cada intervalo de tiempo. La prueba se lleva a cabo comparando la suma de estos valores esperados «específicos de la tabla» con los episodios observados totales. Si los números observados difieren estadísticamente de los esperados, se supondrá que la diferencia en los 2 grupos no es aleatoria. Este enfoque también puede aplicarse a variables explicativas con más de 2 grupos, aunque la prueba estadística es más difícil de calcular a mano y su potencia estadística disminuye a medida que aumenta el número de comparaciones.
Limitaciones de los métodos no paramétricosLos métodos no paramétricos son muy útiles para analizar datos de supervivencia, aunque también tienen limitaciones importantes. No permiten utilizar factores continuos como variables dependientes (deben categorizarse para estimar los riesgos). Siguiendo el mismo razonamiento, los análisis en los que intervienen varias variables de exposición, que pueden ser continuas o categóricas, no son posibles a no ser que se clasifique a cada paciente en una única categoría (p. ej., para 2 factores con 3 categorías, habrá 6 grupos). Este método suele acabar con grupos pequeños, lo que limita cualquier comparación formal. Y lo que es más importante, no hay modo de ajustar los posibles factores de confusión, sino que hay que analizar por separado los grupos definidos por el factor de confusión (así pues, estos métodos se vuelven complicados rápidamente y los grupos se hacen demasiado pequeños para que el análisis sea válido). Teniendo en cuenta todas estas limitaciones, para analizar datos de supervivencia, puede aplicarse un método más avanzado con modelos de regresión.
MODELOS DE REGRESIÓN PARAMÉTRICALos análisis de regresión establecen un modelo matemático para los tiempos de supervivencia, lo que determina de qué modo estos dependen de cada una de las exposiciones (o asignaciones aleatorias). Es análogo a utilizar otro tipo de análisis de regresión, como la regresión lineal para estudiar la dependencia de las variables de respuesta continua con respecto a las variables explicativas, o la regresión logística para estudiar la dependencia de un resultado binario con respecto a las variables explicativas. Los modelos de regresión para datos de supervivencia son paramétricos o semiparamétricos18–20 y ambos proporcionan una medida de efecto conocida como HR. Los modelos presentados en este apartado se definen como paramétricos porque se asume una distribución característica de los tiempos de supervivencia que dependen de determinados parámetros. Por ello, se asume que los tiempos de supervivencia siguen una distribución conocida.
Indicaciones para utilizar modelos de regresión paramétrica para el análisis de datos de supervivenciaLa elección de una distribución teórica para aproximar los datos de supervivencia es tanto un arte como un cometido científico importante, y los modelos de regresión serán siempre una manera simplista de resumir la realidad. Los modelos paramétricos asumen que las funciones de supervivencia y de riesgo tienen una distribución concreta que a menudo es demasiado estructurada y a veces poco realista para utilizar con datos de la vida real21. Es complicado aislar todas las posibles causas que pueden dar lugar a un evento en un momento determinado y explicarlas matemáticamente. Sin embargo, hay algunos contextos en los que es apropiado utilizar modelos paramétricos.
Modelo exponencialEl modelo paramétrico más básico para analizar el tiempo de supervivencia es la distribución exponencial, que se caracteriza por una función de riesgo constante. Según este modelo, observar un evento es algo aleatorio e independiente del tiempo. La distribución exponencial, a la que menudo se hace referencia como un modelo de eventos aleatorio, se caracteriza por su «ausencia de memoria», lo que significa que la probabilidad de que un sujeto sufra un evento en el futuro es independiente del tiempo durante el cual el sujeto no haya sufrido ninguno1. La distribución exponencial se caracteriza por un único parámetro (λ): una tasa de riesgo constante. Así pues, un valor λ alto indica un riesgo elevado y corta supervivencia, mientras que un valor λ bajo indica bajo riesgo y gran supervivencia18. Los modelos exponenciales se utilizan poco en el ámbito cardiovascular, pero se han aplicado en otras áreas, como el cáncer22 o el estudio sobre la deshabituación tabáquica23.
Modelo de WeibullEn muchos contextos, no es razonable asumir una tasa de riesgo constante a lo largo del tiempo tal como se hace en el modelo exponencial18. Por ello, un enfoque alternativo es considerar la distribución de Weibull para parametrizar los tiempos de supervivencia. A diferencia de lo que ocurre en la distribución exponencial, no se asume una tasa de riesgo constante (porque la función de riesgo aumenta o disminuye con el tiempo) y por ello, es un modelo más flexible y con más posibles aplicaciones. Este método se utiliza cuando la función de riesgo aumenta o disminuye de modo regular y, por lo tanto, se caracteriza por 2 parámetros: el parámetro escala λ (el mismo que para la distribución exponencial) y el parámetro de forma γ, que determina la forma de la curva de distribución24. Al añadir el parámetro de forma, la distribución se vuelve más flexible y se adapta a más tipos de datos (para un riesgo que aumenta, disminuye o se mantiene constante). Un valor λ <1 indica que la tasa de eventos disminuye con el tiempo, mientras que con λ > 1 la tasa de eventos aumenta con el tiempo. Cuando el parámetro escala (λ) es igual a 1, la tasa de eventos es constante en el tiempo (Weibull se reduce a un modelo exponencial).
Realidad sobre los modelos de regresión paramétricaLos modelos de regresión paramétrica formulan predicciones uniformes al asumir una determinada función del riesgo y estimar directamente los efectos absolutos y relativos24. Además del modelo exponencial y de Weibull, hay otros modelos paramétricos (p. ej., Gompertz, Lognormal, etc.)18 que no se abarcan en esta revisión porque en la investigación cardiovascular no se suele recurrir a modelos paramétricos para analizar datos de supervivencia. No obstante, hay algunos ejemplos recientes en 2 publicaciones de ECA importantes que emplearon el modelo de regresión de Weibull para evaluar el tiempo hasta el evento de ser asignado al grupo de tratamiento por razones informativas (p. ej., mortalidad)25,26. En el ensayo ENDURANCE, que comparó un dispositivo de asistencia ventricular izquierda de flujo centrífugo con uno de flujo axial en pacientes con insuficiencia cardiaca avanzada y que no cumplían los criterios para un trasplante cardiaco, se utilizó el modelo de Weibull para el evento primario de supervivencia sin ictus incapacitante o retirada del dispositivo por mal funcionamiento o ineficacia27.
MODELO DE RIESGOS PROPORCIONALES DE COXEl modelo de riesgos proporcionales de Cox (RPC) es la estrategia más habitual para evaluar la relación entre las covariables y la supervivencia1,18, y fue propuesto por Cox en 1972 para identificar en los ensayos clínicos diferencias en la supervivencia que se debiesen al tratamiento o los factores pronósticos19,28. Mientras que los métodos no paramétricos analizan la función de supervivencia, los métodos de regresión estudian la función de riesgo.
El RPC es un enfoque semiparamétrico28, dado que en este modelo no se parametriza la función de riesgo inicial, sino el efecto de las variables explicativas en el riesgo (con coeficientes β). Por ello, no se especifica el riesgo basal (no se determinan los parámetros que hay que calcular), por lo que no se hacen presunciones en cuanto a la función de riesgo basal de cada grupo (la supervivencia puede variar entre expuestos y no expuestos en un estudio observacional, o entre el grupo de intervención y el de control en un ECA1), mientras que sí asume que el cociente de sus riesgos sea constante. En conclusión, se parametrizan los efectos de las covariables en la supervivencia, que son constantes y aditivos en una sola escala. Así se puede analizar la asociación entre cada una de las variables independientes y el tiempo de supervivencia ajustando por otras covariables.
Supuestos estadísticos del modeloComo cualquier otro modelo estadístico, el método de RPC se basa en algunos supuestos. Sin embargo, el enfoque semiparamétrico establece menos supuestos que los requeridos para los métodos paramétricos alternativos:
- •
El principal supuesto del modelo de Cox es que los HR (que se definen como el cociente de los riesgos instantáneos entre 2 grupos) son independientes del tiempo; dicho de otro modo, el cociente de los riesgos instantáneos entre 2 grupos es constante en el tiempo y es lo que se conoce como hipótesis de los riesgos proporcionales (RP). Si una variable explicativa tiene fuerte asociación con la supervivencia al inicio del seguimiento pero un efecto posterior más débil, debería considerarse que no cumple la hipótesis de los RP.
- •
El supuesto según el cual se ha especificado correctamente la forma de la variable explicativa obliga a cumplir la hipótesis de los RP, dado que puede cumplirse con una forma concreta de la variable explicativa pero no con otra. Para cumplir este supuesto, las variables explicativas tienen que transformarse en otro tipo de variables. Así pues, las variables continuas pueden categorizarse utilizando un valor discriminatorio binario, por ejemplo en el caso del índice de masa corporal y la hemoglobina, o se debe recurrir a la propia naturaleza de la variable continua y clasificar solo por encima de un determinado umbral, como ocurre, por ejemplo, en el caso de la creatinina y la glucemia29. La situación más habitual es la transformación logarítmica de las variables muy sesgadas.
- •
Los datos censurados son no informativos.
- •
Las observaciones son independientes.
Según todo lo anterior, el modelo de Cox puede ajustarse a cualquier distribución de los datos de supervivencia si el supuesto de los RP es válido (en realidad, la mayoría de los HR tienen una proporción fija), por lo que este modelo acaba siendo el utilizado con más frecuencia.
Comprobación del modelo estadísticoAntes de describir los resultados, conviene comprobar, siempre que sea posible, que el modelo ajustado se ha determinado correctamente. En caso contrario, las inferencias no serían válidas y podrían sacarse conclusiones incorrectas. La comprobación del modelo estadístico de datos de supervivencia no es una tarea fácil. En este apartado, el objetivo es evaluar la hipótesis de los RP y proporcionar algunos métodos para valorar si la forma funcional de las variables explicativas es correcta. Los últimos 2 supuestos no pueden comprobarse formalmente.
Hay 3 modos principales de evaluar si la hipótesis de los RP se sostiene de manera razonable30. El primer método se relaciona con las estimaciones de Kaplan-Meier. Si una variable categórica independiente cumple la hipótesis de los RP, la representación de la función de supervivencia frente al tiempo de supervivencia mostrará 2 curvas paralelas. Asimismo, la gráfica del log(–log[supervivencia]) frente al log de la gráfica del tiempo de supervivencia tendría que dar lugar a líneas paralelas si la variable independiente es proporcional. Este método puede llegar a ser problemático con variables con muchas categorías y no funciona bien con variables continuas, salvo que estén clasificadas. Además, este tipo de análisis se complica más con los modelos multivariantes con varias variables explicativas, que tendrían que comprobarse simultáneamente mediante combinaciones de las covariables31. Así pues, este enfoque es engorroso y poco realista cuando hay más de 2 o 3 variables. El segundo método para comprobar la hipótesis de RP es probar formalmente si el efecto de las variables explicativas en el riesgo cambia con el paso del tiempo (lo cual se hace incluyendo en el modelo una interacción entre el tiempo y la variable explicativa). De modo que una interacción significativa implicaría que la función de riesgo cambia con el tiempo e incumpliría la hipótesis de RP. El tercer modo de evaluar este supuesto es a través de los gráficos de los residuos de Schoenfeld escalados, que son los valores observados menos los esperados de las covariables en cada tiempo de seguimiento31,32. El gráfico de los residuos de Schoenfeld frente al tiempo para cualquier covariable no debería mostrar un patrón dependiente del tiempo.
Además de comprobar el supuesto de los RP, se puede evaluar otros aspectos del ajuste del modelo con residuales30. Pueden utilizarse los residuos de martingala para estudiar las propiedades funcionales para las variables continuas. Un residuo de martingala es la diferencia entre lo que le ocurrió a un sujeto (si sufrió el evento o no) y lo que se predijo que le ocurriría en las condiciones del modelo ajustado33. Puede utilizarse un gráfico de residuos de martingala de un modelo nulo (modelo sin variables explicativas) frente a las variables continuas para indicar la forma funcional apropiada para la variable continua cuando se introduce en el modelo. Los residuos de desviación y otros métodos quedan fuera del alcance de esta revisión.
Recomendaciones finales sobre los métodos no paramétricos, paramétricos y semiparamétricosLos gráficos de Kaplan-Meier son un modo excelente de ilustrar de manera gráfica los datos de supervivencia a lo largo del tiempo, sobre todo cuando la frecuencia del evento cambia de manera irregular en el tiempo. Si se conoce el tiempo exacto de supervivencia de cada paciente o el tiempo hasta la censura, es fácil para los investigadores elaborar los gráficos y para los lectores, interpretarlos. La prueba de rangos logarítmicos es una herramienta simple que proporciona una prueba de significación para comparar los tiempos de supervivencia entre los grupos. No obstante, esta prueba solo proporciona un valor de p pero no una medida del efecto, a diferencia de cualquier método de tipo regresión que proporciona un HR. Otra ventaja del método del HR (ya sea paramétrico o semiparamétrico) es que ofrece instrumentos para investigar los factores de confusión y la modificación del efecto. Así pues, los enfoques no paramétricos sirven para explorar datos y proporcionan estimaciones brutas, pero los métodos de tipo regresión suelen utilizarse para obtener estimaciones más precisas.
Elaborar una estrategia de análisis es una tarea compleja. En los análisis de supervivencia, el hecho de comprobar hipótesis de RP dificulta aún más la estrategia. Esta comprobación puede hacerse en distintos momentos a lo largo del proceso de construcción del modelo estadístico. No obstante, si el supuesto de los RP no se cumple, pueden aplicarse otras opciones analíticas (cambiar la forma de las variables explicativas introducidas en el modelo, utilizar modelos de RPC estratificados o recurrir a otro tipo de metodología, como se explica en la segunda parte de esta revisión).
ESTRATEGIA DE ANÁLISIS ESTADÍSTICO: RECOMENDACIONES E INDICACIONESPara el análisis de datos de supervivencia, pueden utilizarse distintas estrategias, que dependen principalmente del tipo de estudio y la pregunta de investigación por responder. En este apartado, se aportan algunas recomendaciones para el análisis en ECA que se centran en analizar el efecto de un tratamiento y para el análisis de estudios observacionales que se centran en evaluar la relación entre la exposición y los tiempos de supervivencia. Estas recomendaciones no son el único modo de realizar un análisis estadístico correcto, sino que son un resumen de la metodología estadística que abarca todos los aspectos clave.
Ensayo clínico aleatorizadoEn un ECA a gran escala, se asume que no hay variables que pueden confundir la relación entre la intervención aleatorizada y el evento. Una estrategia sensata para evaluar los datos de supervivencia sería: a) describir el número de participantes en los grupos de asignación aleatoria y resumir el número de eventos en cada grupo; b) proporcionar las estimaciones de Kaplan-Meier de las curvas de supervivencia en los grupos de tratamiento y utilizar la prueba de rangos logarítmicos para evaluar la hipótesis alternativa (las curvas de supervivencia difieren entre los grupos de tratamiento); c) utilizar gráficos para evaluar de manera informal si un modelo de RP sería apropiado para obtener una estimación fiable de la relación entre el tratamiento y el tiempo de supervivencia (los gráficos son paralelos cuando los riesgos para ambos grupos son proporcionales); d) si un modelo de RP parece razonable, ajustar un modelo de RPC (o un modelo paramétrico, si procede) para estimar el HR con su IC95% y el valor de p correspondiente, y e) hacer evaluaciones más formales sobre la hipótesis de RP (p. ej., probando si hay interacción entre el efecto del tratamiento y el tiempo o trazando los residuos de Schoenfeld).
Estudios observacionalesLa pregunta de investigación que se plantea en un estudio observacional determina la elección de las variables explicativas que se utilizarán en un modelo de supervivencia. A veces el objetivo es estimar el «efecto» de una exposición: el interés radica principalmente en una exposición concreta, pero se necesitan otras variables para controlar los posibles factores de confusión. En otras ocasiones, el objetivo es comprender las relaciones entre una serie de variables explicativas y el tiempo transcurrido hasta el evento. En este caso, el interés se centra en la relación simultánea e independiente entre varias exposiciones y la supervivencia, quizá para determinar cuál tiene el mayor impacto en esta. Las estrategias para tratar estos 2 tipos de estudios observacionales se presentan en el próximo apartado.
En esta revisión no se abarcan los modelos de predicción, en los que el objetivo es utilizar una serie de variables para construir un modelo y predecir la supervivencia de los sujetos de una nueva cohorte34,35. En este contexto, el término «variable independiente» es más apropiado que «variable explicativa», y la estrategia dedica especial atención a obtener estimaciones precisas para predecir resultados y contribuir a la estratificación del riesgo y la toma de decisiones clínicas. Pueden hallarse más detalles sobre el diseño de modelos de predicción en otras publicaciones34,35.
En el caso de los estudios observacionales cuyo objetivo es estimar el «efecto» de una exposición, se propone seguir 3 pasos basados en un enfoque preliminar, un análisis fundamental y una serie de comprobaciones finales para los supuestos de la modelización. Los análisis preliminares incluirían: a) utilizar gráficos de Kaplan-Meier y pruebas de rangos logarítmicos para evaluar la relación univariante entre cada exposición y el resultado; b) utilizar gráficos no paramétricos y de residuos para una evaluación preliminar de la hipótesis de los RP para cada exposición, y c) evaluar la relación entre la exposición principal y cada posible factor de confusión con un método simple pero visual (p. ej., con tabulación cruzada). Suponiendo que fuera apropiado un modelo de RP (ya sea un modelo paramétrico o más habitualmente un modelo de Cox), el análisis principal incluiría los siguientes 7 pasos: a) ajustar un modelo de supervivencia solo con la exposición principal para estimar la relación univariante; b) ajustar otros modelos de supervivencia con la exposición principal y añadir cada posible factor de confusión, de uno en uno; c) evaluar el impacto que tiene ajustar cada factor de confusión en la relación estimada entre la exposición principal y la supervivencia (p. ej., cambio de magnitud y dirección del HR); d) evaluar si cualquier covariable modifica la relación entre la exposición principal y el evento (p. ej., si hay interacciones); e) ajustar un modelo multivariante para la exposición principal, con ajuste de los factores de confusión (predeterminado según los conocimientos clínicos u observado en el paso c) y para interacciones (observado en el paso d); f) volver a incluir en el modelo, uno por uno, los demás posibles factores de confusión para evaluar si lo son en presencia de otras covariables, y g) añadir al modelo final cualquiera de los factores de confusión importantes observados en el paso f. Por último, antes de notificar formalmente los resultados, deben hacerse otras comprobaciones de los supuestos de la modelización y de su ajuste general (p. ej., probando si hay interacción entre el efecto del tratamiento y el tiempo o trazando los residuos de Schoenfeld del modelo final).
En caso de que no exista una hipótesis previa clara sobre qué variables explicativas pueden relacionarse con la supervivencia, a veces es necesario realizar un análisis exploratorio. Si no hay demasiadas variables, sería razonable incluirlas todas en un modelo y evaluar las relaciones entre cada variable y el resultado después de ajustar para otras covariables. Por otra parte, es útil un proceso similar de 3 pasos basado en un enfoque preliminar, un análisis fundamental y la comprobación del modelo. Los análisis preliminares deben incluir gráficos de Kaplan-Meier y pruebas de rangos logarítmicos para evaluar la relación entre cada variable y el resultado. Después de este primer enfoque, el análisis fundamental tiene por objetivo seleccionar el «mejor» conjunto de covariables. Este enfoque requiere seguir las siguientes tareas: a) evaluar por separado cada variable en una secuencia de modelos de RP (Cox o paramétrico, si procede) para evaluar las relaciones univariantes entre las variables explicativas y el evento; b) incluir todas las variables seleccionadas en el paso anterior en único modelo de RP y a continuación excluir cada variable una por una para evaluar si la exclusión tiene un impacto significativo en la probabilidad logarítmica (la significación estadística puede comprobarse utilizando pruebas de cociente de verosimilitud); c) volver a introducir en el modelo una a una las variables eliminadas en el paso anterior para comprobar si añaden algo al modelo (con pruebas de cociente de verosimilitud), y d) repetir el paso c tantas veces como sea necesario con todas las variables explicativas que queden fuera del modelo en cada «ciclo». Por último, deben hacerse otras comprobaciones de los supuestos estadísticos de cada modelo, tal como se ha explicado sobre otros tipos de análisis.
Otros enfoques para las últimas 2 circunstancias son emplear instrumentos automáticos para seleccionar las variables explicativas, tales como los procesos de selección por pasos hacia adelante o hacia atrás. Aunque en algunos casos son válidos (sobre todo para modelos de predicción), convendría tener claro que el diseño de modelos de regresión tiene un componente tan artístico como científico, lo que requiere conocimientos médicos así como experiencia y conocimientos estadísticos.
CONCLUSIONESEste es el primero de una serie de 2 artículos formativos que revisan los conceptos básicos de los análisis de supervivencia, y establecen los fundamentos para comprender, comparar y aplicar los modelos estadísticos más apropiados para los análisis de supervivencia. Con el objetivo de llegar a los lectores con pocos conocimientos en estadística, en esta revisión se abordan las principales cuestiones del análisis de supervivencia, con ejemplos prácticos de estudios cardiovasculares, que muestran al lector cómo hacer un análisis de supervivencia y cómo interpretar sus resultados. Se explican los supuestos estadísticos de los principales modelos y se proporcionan instrumentos para aplicar el modelo estadístico apropiado según el tipo de datos de supervivencia. Además, también se dan recomendaciones para orientar la estrategia de los análisis, con el objetivo de que el lector pueda en el futuro hacer una evaluación crítica de los datos estadísticos y mejorar su capacidad de análisis. El segundo artículo abordará varios retos estadísticos más complejos a los que a menudo se enfrentan los análisis de supervivencia. Estos son: los riesgos competitivos, los métodos de eventos recurrentes, los modelos multiestado y el uso del tiempo de supervivencia medio limitado.
FINANCIACIÓNNinguna.
CONTRIBUCIÓN DE LOS AUTORESX. Rossello y M. González-Del-Hoyo concibieron la revisión. X. Rossello dirigió el proceso de redacción y M. González-Del-Hoyo se encargó de buscar la mayoría de los ejemplos para ilustrar los métodos. X. Rossello redactó el artículo, aunque ambos autores contribuyeron de manera sustancial en su revisión.
CONFLICTO DE INTERESESNinguno.