Noninferiority randomized clinical trials (RCTs) are usually performed when an experimental treatment is not expected to be more effective than the standard treatment but offers additional benefits. These advantages could consist of a better safety profile, fewer adverse effects, easier administration, less need for laboratory monitoring, or a lower overall cost.1 Noninferiority RCTs vs warfarin include the RE-LY (Randomized Evaluation of Long-Term Anticoagulation Therapy), ROCKET-AF (Rivaroxaban Once Daily Oral Direct Factor Xa Inhibition Compared With Vitamin K Antagonism for Prevention of Stroke and Embolism Trial in Atrial Fibrillation), and ARISTOTLE (Apixaban for Reduction in Stroke and Other Thromboembolic Events in Atrial Fibrillation) studies. This article will review various concepts that are relevant for the interpretation of these studies and all noninferiority RCTs.
WHAT ARE NONINFERIORITY CLINICAL TRIALS?In RCTs, attempts are made to answer research questions with a reasonable degree of certainty. Whereas superiority RCTs aim to determine whether a new treatment is superior to the best available treatment, noninferiority RCTs concentrate on showing that the new treatment is not inferior to the standard one. Thus, the nature of the research question and the possible answers are different. In the specific case of the RE-LY, ROCKET-AF, and ARISTOTLE RCTs, the initial question of interest was: is the new treatment at least as effective as warfarin in reducing thromboembolic events? The 2 possible answers, mutually exclusive and in the form of hypotheses, are as follows:
- •
H0 (the null hypothesis): the new treatment is less effective than vitamin K antagonists in reducing thromboembolic events (it is inferior).
- •
H1 (the alternative hypothesis): the new treatment is at least as effective as vitamin K antagonists in reducing thromboembolic events (it is not inferior).
Adoption of the H0 or H1 “answer” as true involves a decision rule based on the statistical significance of the P value. However, the P value that is calculated in noninferiority RCTs is special, and is called the P value for noninferiority. Let us suppose that the rate of thromboembolic events with the new treatment is lower than with warfarin at a P value for noninferiority of less than .001. In this case, the alternative hypothesis H1 is accepted, because if the new treatment was actually inferior to vitamin K antagonists, obtaining this result would have been as unlikely as P < .001.
In noninferiority RCTs, what is considered “at least as effective as” or “not inferior to” the conventional treatment must be defined a priori. Accordingly, a minimum noninferiority margin or threshold has to be selected. Noninferiority RCTs aim to show that the effect of the experimental treatment is not inferior to that of the standard treatment to “a certain extent”, which is termed the noninferiority threshold or noninferiority margin or delta (δ). The δ value represents the maximum difference tolerated between the effect of the control and the experimental treatment, favoring the former, for the experimental treatment to still be considered noninferior to the control.2
HOW IS THE MINUMUM NONINFERIORITY THRESHOLD δ CHOSEN?The noninferiority margin δ has to be selected according to the best evidence available on the efficacy of the standard treatment compared with placebo,2 taking into account the degree of certainty or uncertainty that is applied to the effect of the standard treatment, which tends to be conservative. The noninferiority margin cannot exceed the smallest effect that the standard treatment, in our case warfarin, could plausibly have vs placebo.
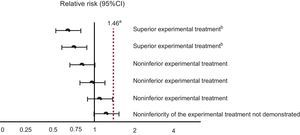
In the case of the new anticoagulants, the minimum noninferiority threshold was selected based on a meta-analysis published in 1999, which quantified the effect of warfarin on the prevention of thromboembolic events vs placebo or absence of treatment, at a relative risk (RR) of 0.38 (95% confidence interval [95%CI], 0.28-0.52).3 The procedure for selecting the threshold is as follows: first, the reference category is changed, as if the effect of the “placebo or absence of treatment” was being calculated with respect to that of warfarin. In our case, this effect would be the inverse of 0.38, which corresponds to an RR of 2.63 (95%CI, 1.92-3.57). The lower margin of this confidence interval (1.92) could be considered the minimum noninferiority threshold for the new anticoagulants. However, the regulatory agencies were more demanding, and chose a noninferiority threshold that assumes that warfarin has a hypothetical effect that is just 50% of its real effect. Accordingly, the minimum noninferiority threshold was set at 1.46, which means that, to conclude that the new treatment is not inferior to the standard one, the upper limit of the 95%CI of the effect of the new treatment compared with that of warfarin cannot exceed 1.46. The possible scenarios that could be obtained in comparisons between the new anticoagulants and warfarin are outlined in Figure 1.
DOES THE STATISTICAL ANALYSIS IN NONINFERIORITY RANDOMIZED CLINICAL TRIALS HAVE ANY SPECIAL FEATURES?Statistical analysis of noninferiority RCTs generally follows a similar methodology to that of superiority RCTs, except that a noninferiority threshold-related P value for noninferiority is calculated, which differs from the P value for “superiority”. Thus, for example, the effect of the treatment on the primary outcome variable “stroke or systemic embolism” in the intention-to-treat (ITT) analysis of the ROCKET-AF trial had a hazard ratio (HR) of 0.88 (95%CI, 0.75-1.03). The P value for superiority was .12, whereas the P value for noninferiority was less than .001, which is unsurprising, given that the noninferiority threshold is to the right of the threshold for the absence of an effect.
An important point for the interpretation of the results of noninferiority RCTs involves the type of analysis performed: ITT analysis, per-protocol analysis, or safety analysis. In the ITT approach, all patients randomized to either treatment arm are analyzed, regardless of whether they actually received the treatment or if there were protocol violations. Safety analyses include patients that received at least one treatment dose, regardless of whether there were protocol violations. Per-protocol analyses include patients that received at least 1 treatment dose without detected protocol violations. Although the regulatory agencies consider ITT analysis to be obligatory in superiority RCTs, they prioritize the use of per-protocol or safety analysis in the investigation of noninferiority hypotheses.2 In noninferiority studies, ITT analysis is usually more “liberal”. In other words, the inclusion of patients with protocol violations or treatment interruptions tends to bias the results toward showing the absence of differences between the treatments, favoring the demonstration of noninferiority.
Finally, can both inferiority and superiority hypotheses be tested in a single RCT? Yes, as long as the α risk is controlled. The α risk value refers to the probability of rejecting H0 when it is actually true. The greater the number of hypotheses that are tested in a study with the same data, the greater the likelihood that a statistical association will be found by chance. Accordingly, to avoid false positives, the α error should be “distributed” among the hypotheses, meaning that the P value has to be lower to find statistically significant results. Appropriate adjustments to the α risk were made in the 3 studies, although the ROCKET-AF analysis had certain peculiarities.
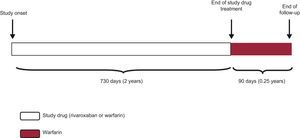
DISTINCTIVE FEATURES OF THE ANALYSIS PLAN OF THE ROCKET-AF TRIALIn the ROCKET-AF trial, ITT, safety, and per-protocol analyses were performed for the main outcome measure (stroke or peripheral embolism), with one peculiarity: both the per-protocol and the safety analyses included only the period when the patient was receiving the experimental drug or the placebo and until 48hours after discontinuation (the as-treated population). This point is important, as the survival analysis method considers the “time-to-event”, and not the proportion of events. Thus, if a patient received the study medication (experimental or placebo) for 730 days (2 years) and was subsequently followed up for a further 90 days (approximately 0.25 years), this patient would contribute 732 days (730 days on medication + 2 days after discontinuation ≈2 patient-years) to the per-protocol and safety analyses, but 820 days (≈2.25 patient-years) to the ITT analysis (Figure 2).
The main noninferiority analysis of ROCKET-AF was performed in the per-protocol and ITT populations. Moreover, safety superiority analysis and various sensitivity analyses were performed to evaluate the noninferiority and superiority of the ITT population, with the appropriate α risk adjustments. Because the main hypothesis is of noninferiority, the appropriate principal analysis is that of the per-protocol population.2 On the other hand, as the international and national agencies acknowledge, analysis of the safety population is suitable for evaluating clinical efficacy, because this population excludes those patients that do not receive the experimental treatment or change to the control treatment. In the ROCKET-AF study, the superiority hypothesis was evaluated in these safety and ITT populations (for the primary outcome: safety population, HR = 0.79; 95CI%, 0.65-0.95; P for superiority = .02; ITT population, HR = 0.88; 95%CI, 0.75-1.03; P for superiority = .12).4,5
ARE THE RESULTS OF THE THREE TRIALS COMPARABLE?Because the 3 trials assess the same noninferiority hypothesis and all use warfarin as control, it is tempting to compare their results. However, any comparison made among them would be an indirect comparison, and the differences in the study populations, the control intervention, and the design are potential sources of bias.6 Accordingly, there were differences in the risk of thromboembolism: the mean risk of thromboembolism measured by CHADS2 was 3.47 in ROCKET-AF compared with 2.1 in both RE-LY and ARISTOTLE. The higher risk of thromboembolism was largely due to the greater inclusion of patients with a history of stroke (55% in ROCKET-AF vs 20% in RE-LY and ARISTOTLE). Moreover, the mean time in therapeutic range of the international normalized ratio (INR) also differed considerably among the studies (55% in ROCKET-AF vs 65% and 62.2% in RE-LY and ARISTOTLE, respectively). Although various analytical techniques have been developed for indirect comparisons, such as network meta-analysis, adjusted indirect comparisons, and the Bucher method,7,8 direct comparison is the only trustworthy method for determining differences in efficacy between drugs. Thus, although some indirect comparisons between studies have been published,9 the differences mentioned in population type, controls, and study design make these comparisons subject to certain biases, and caution must be exercised in their interpretation.
CONCLUSIONSThe use of new oral anticoagulants certainly represents a significance advance in the prevention of thromboembolic phenomena in nonvalvular atrial fibrillation. The RCTs discussed here studied the efficacy and safety of the 3 new drugs, examining both noninferiority (as the primary hypothesis) and superiority hypotheses. Although there is an understandable eagerness to identify the most efficacious, effective, and efficient drug, appropriate direct comparisons are required to reliably obtain this information. It is likely that, as time passes and additional data are obtained from observational studies, the characteristics of the disease, the environment, and, above all, the patient (eg, comorbidities, hemorrhagic risk, psychosocial factors) will continue to be defined, enabling the establishment of the precise indications of each drug for each specific patient group.
CONFLICTS OF INTERESTSThe author has received honoraria for teaching courses and giving academic talks from Boehringer-Ingelheim, Bayer, and Pfizer.
The author thanks Content Ed Net for assisting in the editing of the manuscript.