Randomization of treatment assignment in experiments generates treatment groups with approximately balanced baseline covariates. However, in observational studies, where treatment assignment is not random, patients in the active treatment and control groups often differ on crucial covariates that are related to outcomes. These covariate imbalances can lead to biased treatment effect estimates. The propensity score is the probability that a patient with particular baseline characteristics is assigned to active treatment rather than control. Though propensity scores are unknown in observational studies, by matching or subclassifying patients on estimated propensity scores, we can design observational studies that parallel randomized experiments, with approximate balance on observed covariates. Observational study designs based on estimated propensity scores can generate approximately unbiased treatment effect estimates. Critically, propensity score designs should be created without access to outcomes, mirroring the separation of study design and outcome analysis in randomized experiments. This paper describes the potential outcomes framework for causal inference and best practices for designing observational studies with propensity scores. We discuss the use of propensity scores in two studies assessing the effectiveness and risks of antifibrinolytic drugs during cardiac surgery.
Keywords
In a randomized experiment, the random assignment of patients to active treatment or control leads to treatment and control groups with approximate balance on background measurements such as age, sex, and medical history. We refer to these pretreatment measurements as “covariates.” The covariate balance created by the randomization allows unbiased estimates of the treatment effect. However, randomized experiments are sometimes not feasible for ethical, logistical, financial, or other reasons. In these situations, we can attempt to design studies that parallel randomized experiments as closely as possible, using observational (ie, non-randomized) data.
When patients are assigned to active treatment or control nonrandomly, the treatment groups often differ in important ways on key covariates that are related to outcomes. For example, if the active treatment is considered risky for older patients, then, in general, patients assigned to the control group may be older than patients assigned to the active treatment group. A naive comparison of observed outcomes in these active treatment and control groups would lead to a biased estimate of the treatment effect because of the imbalance in age.
In order to generate unbiased treatment effect estimates using observational data, patients should be grouped (“subclassified”) or matched such that treated and control patients within each subclass or match are well balanced on key observed covariates. Subclassifying or matching on estimated propensity scores can create balance on many observed covariates simultaneously, leading to unbiased treatment effect estimates.1
Propensity score methods have increasingly appeared in cardiology literature.2, 3, 4, 5, 6 Because propensity score techniques are not always implemented correctly, this paper presents the underlying framework and outlines best practices. The first section introduces two examples that we use to illustrate observational study design. The next section explains the potential outcomes framework. We then present best practices for designing an observational study using propensity scores and argue that typical regression modeling is not appropriate for observational studies. We conclude with a discussion of the propensity score methods used in the two examples.
EXAMPLES: APROTININ VERSUS TRANEXAMIC ACIDTo illustrate, we focus on two observational studies that used propensity scores to examine the effects of the serine protease inhibitor aprotinin during cardiac surgery. Karkouti et al.5 and Mangano et al.6 each compared blood loss and adverse event rates among patients receiving aprotinin versus other antifibrinolytic drugs, including tranexamic acid.
Karkouti et al.5 considered 10 949 cardiac patients at the Toronto General Hospital who received either aprotinin (active treatment) or tranexamic acid (control) during cardiac surgery with cardiopulmonary bypass between June 1999 and June 2004. Of these patients, 60 were excluded due to participation in another study, and 19 were excluded because they did not receive either aprotinin or tranexamic acid. Among the remaining 10 870 patients, 586 received aprotinin, and 10 284 received tranexamic acid.
Mangano et al.6 enrolled 5436 cardiac patients from 69 medical centers on 4 continents who underwent coronary artery bypass graft surgery between November 1996 and June 2000.7 Patients either received no antifibrinolytic drugs or received aprotinin, tranexamic acid, or aminocaproic acid. Among patients meeting further eligibility criteria, 1295 received aprotinin and 822 received tranexamic acid.
THE POTENTIAL OUTCOMES FRAMEWORK FOR CAUSAL INFERENCE Potential OutcomesWe limit our discussion to studies comparing two treatment options, though the framework can be extended to more than two treatments. For each patient, there is one potential outcome (eg, serious adverse event or not) that would be observed if the patient were assigned to active treatment and one potential outcome that would be observed if the patient were assigned to control. The fundamental problem of causal inference is that only one potential outcome can be observed for each patient, because each patient is assigned to either active treatment or control, but not both.8, 9 Therefore, causal inference is a missing data problem: the goal is to fill in the missing potential outcomes, estimating what would have happened to each patient had he been assigned to the opposite treatment group.
Any treatment effect estimate either implicitly or explicitly assumes a value for each missing potential outcome. The simplest, naive estimator for the treatment effect is the difference in mean observed outcomes in the active treatment and control groups. This method implicitly assumes that the missing potential outcomes under active treatment for those assigned to control are equal to the mean of the observed outcomes in the active treatment group; and that the missing potential outcomes under control for those assigned to active treatment are equal to the mean of the observed outcomes in the control group.
The use of the observed overall treatment group means to estimate the missing potential outcomes is justified if treatment is assigned completely at random. Otherwise, the missing potential outcomes must be estimated in a way that takes into account the decision-making process for assigning active treatment versus control.
Assignment Mechanism and Propensity ScoresThe assignment mechanism is the decision-making process used to allocate some patients to active treatment and some to control. The propensity score for each patient is the probability that the patient would have been assigned to active treatment rather than control, given his covariates. In a randomized experiment, each patient's propensity score is known. For example, in a completely randomized experiment where half of the patients are assigned to each treatment group, each patient's propensity score is one half. A simple comparison of the observed outcomes in the treatment and control groups would be unbiased in this case.
In a randomized block experiment, patients are grouped together based on their similar observed covariates, and the probability of assignment to active treatment may be different for patients in each block. For example, if the active treatment is considered riskier for older patients, patients over age 65 may be assigned to active treatment with probability 0.4, and patients 65 and under may be assigned to active treatment with probability 0.7. A simple, naive comparison of the observed outcomes in the active treatment and control groups would be biased because the active treatment group would contain a disproportionate number of younger patients. To generate unbiased treatment effect estimates, we would compare patients assigned to active treatment versus control within each age group. Patients in each age group have the same propensity score. By estimating treatment effects within each age group, we implicitly fill in each patient's missing potential outcome based on the observed outcomes of other patients in the same age group.
In an observational study, it is still true that grouping patients with similar propensity scores leads to unbiased treatment effect estimates. However, the probability that any particular patient would be assigned to active treatment versus control, given his covariate values, is unknown when treatment is assigned nonrandomly. The researcher may be reasonably satisfied that all covariates that could have affected the treatment assignment decision are included in the data set. If so, we call the assignment mechanism unconfounded, and we can estimate the unknown propensity scores based on these observed covariates. By comparing patients with similar estimated propensity scores, we can design an observational study that resembles a randomized experiment.
In the study described by Karkouti et al.,5 the decision-making process for assigning an antifibrinolytic drug was based on known guidelines. Physicians at Toronto General Hospital were advised to use aprotinin only for a subset of high-risk patients and to use tranexamic acid otherwise. Because the guidelines informed but did not determine treatment decisions, there is a subset of patients who might have received either aprotinin or tranexamic acid. This subset of patients, who had some chance of receiving either treatment, is necessary for designing an observational study that could lead to unbiased treatment effect estimates. The hospital's guidelines provide a useful starting point for estimating the assignment mechanism and propensity scores.
Because of the broad geographic scope of Mangano et al.,6 the assignment mechanism is likely more complicated. The treatment decision-making process may have functioned differently within each of the 69 institutions included in the study.
DESIGNING AN OBSERVATIONAL STUDY Identifying Timing of Treatment AssignmentThe first step in designing an observational study is identifying the time of the treatment assignment. In a randomized experiment, it is typically easy to identify the time when each patient was randomly assigned to active treatment or control via a coin flip, an opened envelope, a computer, etc. Pinpointing the time of treatment assignment in an observational study can be more difficult. If the physician chose active treatment or control for a particular patient, then the moment of this decision is the time of the treatment assignment. Alternatively, the patient may have self-selected into the active treatment or control group, and the timing of that decision relative to other observed measures must be identified.
The timing of the treatment assignment is important because it allows us to distinguish pretreatment (“proper”) covariates from posttreatment (“improper”) measurements. Proper, pretreatment covariates are measured or could be measured before treatment is assigned. Medical history prior to the treatment decision is a proper covariate. Age and sex are also covariates, even if actually recorded after the treatment decision, because age and sex could not be affected by the treatment.
Any other information measured after treatment assignment is an outcome. Primary outcomes may include death, blood loss, adverse events, etc. A patient's blood pressure the day after self-selecting into the active treatment or control group is also an outcome rather than a covariate, even if the effect of treatment on this blood pressure measurement is not of interest.
An observational study design should create balance on pretreatment covariates, because, on average, randomization would lead to balance on pretreatment covariates in an experiment. However, we should not attempt to create balance on posttreatment measurements, because posttreatment measurements could be impacted by the active treatment or control. This distinction is crucial: misclassifying an outcome that could have been affected by treatment as a proper covariate can mask the treatment effect.
For example, consider a study comparing two antifibrinolytic drugs given during cardiac surgery, where the outcome of interest is bleeding two days after surgery (day 2). Suppose that bleeding one day after surgery (day 1) strongly predicts bleeding on day 2. If bleeding on day 1 is misclassified as a proper covariate, we would group the patients by day 1 bleeding. Because of the strong correlation between day 1 and day 2 bleeding, grouping patients by day 1 bleeding masks the true treatment effect: among patients with bleeding on day 1, most would have bleeding on day 2, regardless of treatment assignment, and among patients without bleeding on day 1, most would not have bleeding on day 2, regardless of treatment assignment. Even if there is a large effect of treatment versus control on both day 1 and day 2 bleeding, erroneously conditioning on day 1 bleeding leads to an estimate of no effect because day 1 bleeding predicts day 2 bleeding.
Because antifibrinolytic drugs are transmitted during surgery, the treatment decisions in the studies reported by Karkouti et al.5 and Mangano et al.6 likely took place prior to surgery. Both studies conditioned on measurements that could have been affected by the antifibrinolytic drug. Several of the medication indicators considered for the models generated by Mangano et al.6 are classified as intra-operative.7, 10 The propensity score model in Karkouti et al.5 included cardiopulmonary bypass duration, which could have been impacted by a drug transmitted at the beginning of the surgical procedure.
Separation of Design and AnalysisThe randomization protocol for an experiment is necessarily finalized before outcomes are collected. In order to mirror a randomized experiment, the design of an observational study should similarly be separated from the outcome analysis. Outcomes should be removed from the data set before study design begins, as soon as the time of the treatment assignment has been identified.11, 12 Separating observational study design from outcome analysis protects against actual or suspected bias on the part of the researcher.
Identifying and Prioritizing CovariatesBefore designing an observational study, and if possible before collecting data, experts in the field should identify the covariates that might predict the treatment decision and/or the outcomes. Note that in order to preserve objectivity, this discussion should take place without access to outcome data from the current study, though previous literature may help guide the selection of covariates. If the treatment decision may have been influenced by a covariate that was not collected or is otherwise not available, it will be impossible to determine whether the treatment groups are balanced on that covariate, and the data set may not be useful for addressing the study question. Such an assignment mechanism is confounded, given the observed covariates.
If all of the covariates thought to be importantly related to the treatment decision and outcomes are available, these covariates should be divided into priority groups. Like a randomized experimental design, an observational study design will lead to better balance on some covariates than others. The prioritization of covariates serves as a guide for comparing various proposed observational designs.
Key covariates that are often overlooked in medical studies include date of enrollment and clinical center. Karkouti et al.5 indicated a trend over time in the probability of receiving aprotinin; however, as the authors point out, enrollment date was not included as a covariate. When data is collected over a period of time, medical advances and guideline changes can affect patient outcomes, and it can be important to compare patients with similar enrollment dates.
The 69 separate sites represented in the Mangano et al. study6 may have differed in ways likely to predict outcomes, including staff training and protocols, equipment, and cultural influences. The study design could have been improved by conditioning on the multiple clinical centers.
Addressing Imbalance on a Single Covariate Subclassifying on One CovariateSubclassifying patients on a single, categorical covariate is straightforward. For example, if an observational study includes both men and women, and sex is expected to predict outcomes, then the effect of active treatment versus control can be estimated separately among men and among women. The within-sex treatment effect estimates can be averaged together to estimate the overall treatment effect in the population. Subclassification on a single covariate removes the bias due to this covariate: the missing potential outcome that would have been observed under active treatment for a man who actually received control is estimated using the observed outcomes for men only, rather than the entire sample of men and women.
This approach extends in a simple way to a single, continuous covariate. Patients could be subclassified based on age groups, for example. Five subclasses are typically enough to reduce 90% of bias on a single, continuous covariate.13
Often, some patients in one treatment group are unlike any of the patients in the other treatment group on a key covariate. For example, patients over age 65 may not have been eligible for the active treatment, or one of the clinical centers in a multicenter study may have prescribed the active treatment for all patients. There is no useful information available for imputing these patients’ missing potential outcomes: what would have happened to patients over 65 had they been assigned active treatment, and what would have happened to patients at the all-active-treatment clinic had they been assigned control? Patients without counterparts in the opposite treatment group should be removed from the data set, as the study cannot be designed to generate useful estimates of the effect of treatment for these patients.
Matching on One CovariateMany observational studies include a relatively small group of patients who received the active treatment and a large pool of control patients who did not receive the active treatment. The control patients may come from a surveillance database or another source separate from the treated group. Typically, the majority of control patients have covariate values very different from the treated patients’ and would not have been included if the data had been collected for the purpose of addressing the particular research question. In this situation, a matching control patient may be identified for each active treatment patient based on an important covariate, creating a matched pair design that approximates a randomized pair experiment. Unmatched potential controls can be discarded. The matched pair design leads to unbiased estimates of the treatment effect for patients with covariate values similar to those in the active treatment group. The observed outcome of each matched control patient is used to estimate the missing potential outcome for a matched treated patient.
Crucially, the matched pair design we describe is fundamentally different from a case-control study (or, to avoid confusion, a “case/noncase study”). In a case/noncase study, a patient with a positive outcome is paired to a patient with a negative outcome; both patients may have received active treatment, or both may have received the control treatment. This pairing relies on observing the outcomes and does not parallel any randomized experimental design. In the matched pair design we describe, a patient who received active treatment is paired to a patient who received the control treatment. Matching active treatment and control patients does not require outcome data and parallels a randomized experiment in which pairs of patients with similar observed covariates are randomized, one to active treatment and one to control.
Of course, in most studies, more than one covariate is expected to be related to outcomes. Covariate balance may be desired on age, sex, a variety of medical history indicators, etc. Simultaneously matching or subclassifying patients on multiple covariates quickly becomes unwieldy: with 5 age groups, 2 sexes, and 5 binary indicators for prior medical conditions, 320 separate subclasses would be needed. With 5 more binary indicators for additional demographics or prior medical conditions, over 10 000 subclasses would be needed. The purpose of estimating propensity scores is to simplify this process and create approximate balance on many covariates at once.
Matching or Subclassifying on Estimated Propensity ScoresThough true propensity scores are unknown in observational studies, the propensity scores can be estimated by modeling the probability of assignment to active treatment given the observed covariates, without access to outcomes.1 Propensity scores are most commonly estimated via logistic regression.12 The fitted values from the logistic regression are the estimated propensity scores.
Just as each patient has an age and a sex, each patient has an estimated propensity score, a single number between 0 and 1 representing the estimated probability that someone with that patient's covariates would have been assigned to active treatment rather than control. By matching or subclassifying patients with similar estimated propensity scores, approximate balance can be created on all of the covariates included in the propensity score model.1, 14, 15
The success of the propensity score model and matching or subclassification method should be evaluated by explicitly checking the covariate balance in the proposed design. If treated and control patients were matched based on similar estimated propensity scores, we can check that the matched patients have sufficiently similar ages, medical histories, etc. If patients were sorted by estimated propensity scores and divided into subclasses based on estimated propensity score cutoffs, we can check that active treatment and control patients within each subclass have similar covariate values. The means of the observed covariates should be approximately the same in the active treatment and control groups after matching, or within each subclass and when averaged across subclasses. The variances, ranges, logs, and squares of the continuous covariates should be balanced, and interactions between covariates should be balanced as well.
Because the outcomes are separated from the data set during this design process, we can iterate between estimating the propensity score, creating subclasses or matches, and checking covariate balance. If a particular covariate is not sufficiently balanced after the first proposed design, a revised propensity score model might include interactions between this covariate and other covariates, or the log or square of this covariate if it is continuous. Choosing a particular set of subclasses or matches requires tradeoffs: some proposed designs will achieve better balance on certain covariates and less desirable balance on others. The covariate priority groups should serve as a guide for comparing possible study designs.
Five propensity score subclasses based on quintiles of the estimated propensity scores are typically enough to reduce 90% of bias on all of the covariates used in the propensity score model.14 If the sample size is large or if some covariates are not sufficiently balanced, more than 5 subclasses can be created. When the relative active treatment and control sample sizes and initial balance are such that matching is more appropriate than subclassification, matching each of the active treatment patients to the control patient with the most similar estimated propensity score typically leads to approximate covariate balance,1, 15, 16 but if the balance in the proposed design is not satisfactory, the study can be restricted to pairs of patients within a certain maximum distance of each other on the estimated propensity score.
Importantly, a proposed observational study design should not be evaluated based on how closely the propensity score model fits the data or how well the propensity score model describes the presumed true decision-making process. Estimating the propensity score model is one step toward creating well-balanced subclasses or matches, and the best propensity score model is the one that leads to the design with the best covariate balance.
Rigorous observational study design requires limiting the study to a well-defined sub-sample of the data in which some patients received active treatment and some received control, as in a randomized experiment. If the covariates included in the propensity score model are strongly related to the treatment assignment, some patients may have extreme estimated propensity scores that are outside the range of the estimated propensity scores of patients in the other treatment group. This situation parallels lack of overlap on a single covariate: no information is available to estimate the missing potential outcomes for patients outside the range of overlapping estimated propensity scores. Often, it is possible to determine the covariate values characterizing the patients with extreme propensity scores (for example, perhaps men under a certain age almost always received active treatment and therefore have high estimated propensity scores). Patients meeting these criteria should be removed from the study. Removing patients based on covariate values rather than estimated propensity scores simplifies the study's generalizability.
Because outcomes are not available during observational study design, the proposed matches or subclasses can and should be circulated among and approved by clinicians and other stake-holders. Any objections to the balance on observed covariates in the proposed design should be addressed before the outcome analysis. This process is similar to seeking approval for a randomized clinical trial before beginning enrollment: in the absence of outcomes, modifying the study design cannot bias the final treatment effect estimate.
After a design is finalized, outcomes can be analyzed. In a matched design where patients assigned to active treatment have been paired with patients assigned to control, the observed outcomes in the matched treatment and control groups can be directly compared. In a subclassified design, the observed active treatment and control outcomes can be compared within each subclass, and an overall estimate can be obtained by a weighted average of the within-subclass treatment effect estimates.
THE DANGERS OF REGRESSION IN OBSERVATIONAL STUDIESRegression, also known as covariance adjustment, is frequently used to address covariate imbalance in observational studies. Researchers applying regression methods often include both the treatment indicator and the observed covariates in a model to predict the observed outcomes. However, if covariates are not well balanced initially, this regression adjustment is likely to rely upon invalid assumptions and can sometimes increase instead of decrease bias.1, 17, 18 Unless the outcomes can be predicted accurately from the covariates using straight lines, and unless the effect of treatment is the same for each patient, the estimates for the missing potential outcomes implied by regression can be misleading or nonsensical.
Because of the strong modeling assumptions, regression generates treatment effect estimates even when common sense suggests that information is insufficient. For example, even if the oldest patient who received active treatment is aged 30, regression software will extrapolate (usually based on a straight line) to estimate what would have happened to an 80-year-old in the control group, had he received active treatment.
Regression often leads to relatively narrow confidence intervals for the treatment effect. Though a narrow interval is desirable when the interval is expected to be centered around the true treatment effect, regression adjustments in observational studies often lead to deceptively small intervals around the wrong treatment effect. The narrow intervals reflect the (typically invalid) modeling assumptions rather than information in the data.
Regression estimates are sensitive to the relative sample sizes of the observed active treatment and control groups. If the data includes a relatively small set of treated patients and a large pool of controls, the regression model will primarily be determined by the relationship between the outcomes and the observed covariates among control patients, even if most of these control patients were nothing like the patients who received active treatment.
The most important flaw of regression adjustment for causal inference in observational studies is that study design is not separated from outcome analysis. How often does a researcher run only one regression model? It is tempting to fish for a certain result, fitting several models until the desired or expected answer appears. Because outcomes and covariates are not explicitly separated, it is also easy to ignore the timing of the treatment assignment and include variables that are actually outcomes as predictors in the regression model.
Regression models are sometimes appropriate as part of the outcome analysis, after a matched or subclassified design has been finalized. Given balance on observed covariates, the treatment effect estimate will be approximately unbiased with or without regression, and regression can be an effective way to produce narrow intervals around the right answer.
PROPENSITY SCORES TO COMPARE APROTININ VERSUS TRANEXAMIC ACID Matching in Karkouti et al.In Karkouti et al.,5 patients who received aprotinin rather than tranexamic acid were more likely to be female; without a history of unstable angina, hypertension, or diabetes mellitus; and with a history of congestive heart failure, recent cardiac catheterization, or atrial fibrillation, among other covariates. Karkouti et al.5 created matched pairs of aprotinin and tranexamic acid patients using estimated propensity scores to create balance on observed covariates.
Propensity scores were estimated with a logistic regression model that predicted treatment status from 20 observed covariates, including several interactions. (At least one of these covariates may have been measured posttreatment.) The authors identified tranexamic acid matches for 449 of the 586 aprotinin patients based on similar estimated propensity scores, discarding 137 unmatched aprotinin patients who were not similar to the tranexamic acid patients on the observed covariates.
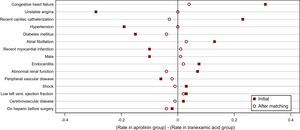
Figure 1 shows the differences in the rates of binary, patient-related covariates between the aprotinin and tranexamic acid groups, before and after matching. The balance on these observed covariates is much better after matching than before matching. In particular, unstable angina within 30 days of surgery was less common in the initial aprotinin group than in the initial tranexamic acid group by approximately 30 percentage points. However, the rates of unstable angina among matched aprotinin patients and among matched tranexamic acid patients are similar. Congestive heart failure was more common in the initial aprotinin group than in the initial tranexamic acid group by approximately 30 percentage points, but the congestive heart failure rates are similar in the matched aprotinin and matched tranexamic acid groups. Note also that the imbalance between the aprotinin patients and tranexamic acid patients on presurgery heparin usage actually increased due to matching. Selecting a final set of matches requires prioritizing the observed covariates, and a different set of matches could have been chosen if the imbalance on heparin usage had been deemed unacceptable during study design.
Figure 1. Differences in rates of binary, patient-related covariates between aprotinin and tranexamic acid groups before and after matching, in Karkouti et al. 5
The generalizability of the study is limited to the population of patients with covariate values similar to the matched patients’. The matched patients are older, more likely to have hypertension and unstable angina, and less likely to have recent cardiac catheterization or endocarditis. The matched patients also have higher hemoglobin concentrations than the initial group of patients who received aprotinin. Because the highest-risk patients who clearly met the hospital's criteria for aprotinin do not have many counterparts in the tranexamic acid group, the matched aprotinin patients are somewhat healthier than the initial aprotinin group.
Karkouti et al.5 found similar rates of transfusion and adverse events among the matched aprotinin and tranexamic acid patients, except that renal dysfunction occurred significantly more often in matched aprotinin patients than in matched tranexamic acid patients.
Regression in Mangano et al.In Mangano et al.,6 patients with a history of congestive heart failure, pulmonary disease, or valve disease, among other covariates, appear to have had a higher probability of receiving aprotinin than tranexamic acid. Rather than create matches or subclasses based on estimated propensity scores, Mangano et al.6 fit a model to regress the observed outcomes on the estimated propensity scores. Regressing observed outcomes on an estimated propensity score is very similar to regressing observed outcomes directly on the covariates included in the propensity score model.1 This use of estimated propensity scores has at times been suggested by statisticians,17 but later corrected.19 Regression on estimated propensity scores shares the disadvantages of regression adjustment discussed above, and the use of estimated propensity scores to create matches or subclasses as part of study design rather than analysis is recommended instead.20
Mangano et al.6 concluded that aprotinin and tranexamic acid led to similar blood loss, but that aprotinin was associated with a higher risk of renal failure, myocardial infarction or heart failure, and stroke or encephalopathy.
CONCLUSIONSMatching or subclassifying on estimated propensity scores can lead to approximate balance on observed covariates between active treatment and control groups in observational studies. Critically, observational studies should be designed without access to outcome data. By designing observational studies that parallel randomized experiments, we can generate unbiased estimates of treatment effects despite the nonrandom assignment of patients to treatment groups.
CONFLICTS OF INTERESTNone declared.
Acknowledgements
Authors are grateful to Valeria Espinosa Mateos for her generous assistance with the Spanish version of this article.
Corresponding author: Department of Statistics, Harvard University, 1 Oxford Street, 7th Floor, Cambridge, MA 02138, United States. rubin@stat.harvard.edu