Keywords
INTRODUCTION
There is much interest in being able to recognize and diagnose ischemic heart disease in its earliest stages; the later disease is detected, the less effective the different treatment alternatives become. Such interest lends itself to a more aggressive use of stress tests, the results of which help in making treatment decisions --decisions that have an enormous social and economic impact when patient populations are large. With increased access to such testing now available, it has become necessary to reappraise the clinical implications of the results (both with and without images) that might be obtained. This paper reviews the concepts behind the use of stress tests to help diagnose ischemic heart disease in daily clinical practice, as well as the implications of the results obtained.
SENSITIVITY AND SPECIFICITY
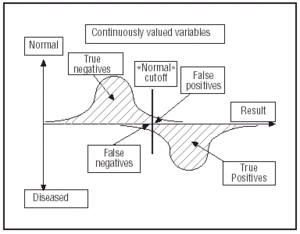
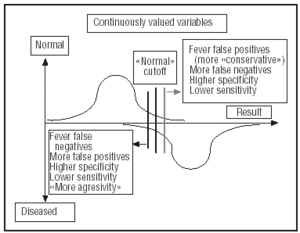
It is important to understand that the interpretation of stress test results is something of a balancing act between art and science. Even though there are established criteria for differentiating between normal and abnormal results, the differences are not always well defined. This is one of the difficulties of using stress tests in the diagnosis of ischemic heart disease, and in good measure it accounts for the variability in the conclusions of those who interpret them. The reason for these problems lies in the fact that the definition of an abnormal test is not based on a strict, defined feature. In many tests, including stress tests, true and false positives and negatives are based on continuous variables (Figure 1) rather than on fixed values. This raises the question of how one defines the upper and lower limits of normality. The experience of the observer, and how «aggressive» or «conservative» he/she is (Figure 2) in terms of maximizing diagnostic sensitivity (i.e., detecting the proportion of patients with the disease through a positive result), plays an important role in this. As a rule, increased sensitivity (by taking an aggressive interpretive stance) is usually accompanied by a reduction in specificity (the proportion of patients without the condition and which actually had a negative result).
Fig. 1. Frequency distribution of a diagnostic test based on a «normal» cutoff, based on continuous variables. Reproduced by permission of the author, Edward Shortliffe, Columbia University, New York, USA.
Fig. 2. Changes in the results of a diagnostic test depending on whether the interpreter is either «more strict» (higher specificity) of «less strict» (higher sensitivity) in the interpretation of the test. Reproduced by permission of the author, Edward Shortliffe, Columbia University, New York, USA.
Any additional information that helps clinicians make a diagnosis with respect to heart disease can modify their interpretation of future stress test results. Correlating the interpretation of the latter with coronary angiography results is essential in both initial and continuing training of medical staff. Auxiliary information is often used in the interpretation of stress tests. For example, as well as the post-stress electrocardiographic or myocardial flux responses, and indications of regional or global function (as in stress tests which provide images), the characteristics of the pain suffered by the patient (if experienced during the test) and the duration of exercise, etc. are important. Even more important is the patient's pretest clinical information, which can influence both the sensitivity and specificity of the test as well as its predictive power (both positive and negative).
BAYESIAN PARADIGM
The concepts discussed by Bayes1 in his work published in 1763 have been used in many ways in cardiology, but particularly with respect to how stress tests should be interpreted when used in the diagnosis of ischemic heart disease.
The Bayesian paradigm2 allows the a priori probability of disease being present to be taken into account and related to the information obtained from a diagnostic test. This provides more objective inferences with which one can calculate the a posteriori probability of disease being present. This is equivalent to the (positive or negative) predictive power of the test, and allows more exact conclusions be drawn from the test results. In essence, the Bayesian paradigm establishes that the confidence one can place on any diagnostic test is defined by its sensitivity and specificity, but more importantly, that the certainty with which a test can confirm a disease depends on its prevalence in the population to which the patient belongs.3,4 Knowing the prevalence of a disease and the sensitivity and specificity of the tests used allows one to calculate the probability that a patient with a positive result actually has the disease. One can therefore calculate the probability that a patient actually has a given condition when his/her test results are positive (positive predictive power) as well as the probability that he/she does not have the disease when the test results are negative (negative predictive power). In clinical practice, knowledge is required in order to make decisions on clinical management, on changes to therapy, or when recommending angioplasty or surgery --and it is vital to know the likelihood that a patient really has the problem the test results suggest. Herein lies the difference in the Bayesian focus. In clinical practice it is also important to know the positive or negative predictive power of the diagnostic tests used, not just their sensitivity or specificity.
In current medical practice, great emphasis is placed on defining the practical impact of and the justification for5 any diagnostic tests used, as well as their cost-effectiveness.6 The idea is that the optimum use of a test should provide information in excess of that which can be gleaned from clinical data alone. The argument often used against Bayesian concepts (and which reflects the main difficulty in their use) arises from the need for prior information on the disease in the form of a working model, its prevalence (the a priori probability), or the proportion of subjects known to have the disease before the test was done. Such information can be subjective. However, with respect to the clinical use of stress test results in the diagnosis of ischemic heart disease, external data are available from studies, based on the examination of hundreds or thousands of patients, that establish a correlation between angiographically-confirmed, significant coronary artery obstruction and clinical data. The American Heart Association, in collaboration with the American College of Cardiology, have published these data7 in guidelines for the clinical assessment of patients. This study8 took into account the sex of the patients, plus the characteristics of any precordial pain. The results were similar to those obtained in the CASS (Coronary Artery Surgery) trial,9 and later confirmed by Pryor et al10 (Table 1).
This table has been adapted from the various guidelines available,7,9 and the values it contains refer to the percentage of persons with significant obstruction as confirmed by coronary angiography. Factors other than those mentioned in the table that increase the number of patients identified with angiographically-confirmed ischemic heart disease include a history of smoking, electrocardiographic abnormalities at rest (Q waves or changes in the T wave or the ST segment), hypercholesterolemia and diabetes (the greatest risk factor). The clinical description of chest pain has been the subject of work by other authors11 who describe the pain of classic angina as retrosternal, as a feeling of heaviness or pressure on the chest, or sometimes as a burning sensation provoked by stress or emotions. This pain is rapidly alleviated by rest or nitroglycerin. The pain of nonclassic or atypical angina is a stabbing sensation in the left side of the chest, abdomen, back or arm, with no manifestation in the center of the chest. It is not related to exercise and does not improve with nitroglycerin but rather with antacids. It is sometimes described as palpitations without chest pain.
The a priori probability expressed as a percentage in Table 1 can also be expressed as the number of times an event happens over the number of times it does not happen i.e., the odds ratio (OR). To lend coherence to the ideas in the different sections of this review, let us examine the hypothetical case of a 52-year-old woman who presents with clinical nonclassic or atypical angina. Table 1 shows that 31.1% of similar patients to have significant coronary obstruction. This figure can also be expressed as the probability of the condition being present over the probability that it is not present (range=0-1), i.e., OR=0.31 divided by 1 minus the OR that it is present (1-0.31=0.69):
OR before the test=0.31/1-0.31
=0.31/0.69, or 0.44
Once the a priori probability is known, it needs to be adjusted to render a likelihood ratio. This depends on the trustworthiness of the diagnostic test being used (in this case the stress test) with respect to its yield of true negatives and positives. The likelihood ratio of a test has both a positive and a negative expression, which are defined in the following way:
Positive likelihood=sensitivity/(1specificity)
(the probability of the test being positive for a patient who has the disease, over the probability that a positive result is obtained for a healthy person).
Negative likelihood ratio=(1sensitivity)/specificity
(or the probability that the test will give a negative result for someone who really has the disease, over the probability that it will give a negative result for a healthy person).
From these definitions it is can be deduced that the best diagnostic test is that with the highest positive and the lowest negative likelihood ratio.
If our hypothetical patient undergoes a diagnostic test with a sensitivity of 85% and a specificity of 75% (according to reliable clinical assays or meta-analyses), then its likelihood ratios can be determined thus:
Positive likelihood ratio=0.85/(10.77)
=0.85/0.23, or 3.69
Negative likelihood ratio=(10.85)/0.77, or 0.19
Once in possession of the likelihood ratios and the a priori probability, the a posteriori probability (the predictive power of the test) can be determined. This can tell us both the proportion of individuals who have the disease and who will obtain a positive test result (positive predictive power), and the proportion of individuals who do not have the disease and who will obtain a negative result (negative predictive power).
Specifically, the
OR after a test=OR before the test x likelihood ratio
To calculate the OR after a positive test, one multiplies the OR before the test by the positive likelihood ratio. In the same way, to calculate the OR after a negative test, one multiplies the OR before the test by the negative likelihood ratio.
According to the clinical example described above:
OR after a positive=0.44 x 3.69, or 1.62
A posteriori probability=1.62/(1+1.62)
=1.62/2.62, or 0.619 (approximately 62%)
In other words, a positive result in the diagnostic test in this patient has a positive predictive power of 62% --much greater than the a priori probability of 31% based on clinical information alone.
Similarly, if the test had been negative:
OR after a negative test=0.44x0.19, or 0.08
A posteriori probability=0.08/(1+0.08), or 0.074 (approximately 7.4%)
Performing the test with this patient would lead to large deviations from the a priori probability, suggesting that it might provide very useful information and significantly alter the predictions that could be made from clinical data alone.
PRACTICAL CONSIDERATIONS
The clinical case described illustrates how to make optimal use of stress tests for patients in whom ischemic heart disease is suspected. In clinical practice, patients are generally classified as having either very low (2-12%), low (4-22%), intermediate (13-76%) or high (>87%) a priori probability. These are approximate, non-numerical data12 but are used in Table 1.7,9 Although it is very common to speak of a very low, low, intermediate or high likelihood of ischemic heart disease, it is important to be aware of the range of numerical values corresponding to these classifications. In the example used here, the patient was classified with intermediate probability, and therefore performing the test was very useful. For patients with very low, low or high a priori probability, performing the test would not be so helpful. In a patient with low a priori probability, a positive test would not change the predictive power. Similarly, in patients with high a priori probability, a negative result would not reduce their chances of actually having the disease.
Further practical considerations can be derived from the meta-analyses13,14 shown in Table 2, and from accumulated clinical experience.15
In patients with symptoms or in those with atypical pain, a negative stress test (especially if echocardiographic or nuclear medicine images are available) can almost completely rule out ischemic heart disease. If the test were positive, but only at high stress levels (e.g., after 12 min on the treadmill using the Bruce protocol), the chance of there being significant heart disease (e.g., of the main trunk of the anterior descending coronary artery, or obstruction of three vessels) would be low. Therefore, such patients have a good long-term prognosis. Only if the test were markedly positive in the electrocardiogram and in the images --and at low stress-- would coronary angiography be justified. If the a priori probability is intermediate in someone who is free of symptoms, tests providing images would be more helpful.
In patients with nonclassic or atypical angina, the a priori probability is intermediate --around 50% if all ages and both sexes are taken into account. If a patient has two positive stress tests, this might increase to as high as 90%. If, however, both tests were negative, it may decrease to just 5%. If there were variations or discrepancies, the case would have to be individually reviewed. Patients with atypical pain and with abnormal images or high cardiac frequency at low stress have a greater chance of having ischemic heart disease than do those with only subtle image abnormalities and no pain at high stress levels. In patients with classic angina, the a priori probability is more than 90% if all factors are taken into account. In such cases, stress tests are used not so much to dia gnose or rule out ischemic heart disease, but to evaluate how serious the patient's condition is and to provide a prognosis. This can guide coronary angiography and percutaneous revascularization by identifying the areas of the myocardium at greatest risk.
CONCLUSIONS
This paper provides some perspective on the practical use of stress tests in cardiology after the clinical evidence is in hand. It does not, however, examine important areas such as diagnosis by magnetic resonance imaging with drug stimulation, or (electron beam) computerized tomography. Although these have great merit and are perhaps more important than echocardiography or nuclear medicine, they are more recent techniques and have not been the subject of frequent meta-analyses. Clinicians should rely on the expertise of their work environment, and base their diagnoses on the type of results with which their hospital has the most interpretive experience. They should also maintain their efforts to correlate any results obtained with the findings of coronary angiography, bearing in mind that this can also be affected by variations in subjective interpretation.
Section sponsored by Laboratorio Dr. Esteve
Correspondence: Dr. J.E. Pérez.
Cardiovascular Division. Washington University,
660 South Euclid, Box 8086, St. Louis, MO 63110, USA.
E-mail: jperez@im.wustl.edu