Hemos leído con atención el artículo de Aranceta-Bartrina et al1., cuyo objetivo era «describir las prevalencias de obesidad total y obesidad abdominal en una muestra representativa de la población española».
Suponemos que el objetivo real de los autores no era conocer la prevalencia de obesidad en la muestra obtenida, sino la verdadera prevalencia de obesidad en la población española. Para ello, seleccionaron una muestra de 3.966 pacientes procurando que fuera representativa, y a partir de ella calcularon el porcentaje de pacientes con obesidad. En un intento de extrapolar estos resultados a la población española, calcularon los intervalos de confianza del 95%.
La estadística frecuentista basada en pruebas de significación, intervalos de confianza y contrastes de hipótesis se encuentra ampliamente implementada en nuestros días. Su principal ventaja es que es sencilla y de fácil reproducibilidad, ya que muchos de sus cálculos se pueden realizar a mano. Su principal desventaja es que no contesta de forma racional a preguntas clínicas. A la pregunta inicial: ¿cuál es la verdadera prevalencia de obesidad en la población española?, no se puede contestar de modo inteligible utilizando este tipo de estadística.
Los autores1 señalan que la tasa de obesidad fue del 21,6% (intervalo de confianza del 95%, 19,0-24,2%). Para entender este intervalo, habría que imaginar repetidas muestras extraídas según el mismo modelo de tal forma que el 95% de tales muestras producirían intervalos que incluirían el verdadero valor poblacional2. Aunque resulte difícil de entender, esto no significa que haya un 95% de probabilidades de que la prevalencia de obesos en la población española se encuentre entre el 19 y el 24,2%, por lo que no se resuelve la pregunta inicial.
La estadística bayesiana es la alternativa a la estadística frecuentista. Es más compleja y puede requerir simulaciones de Markov Chain Monte Carlo2,3, pero tiene la ventaja de responder de modo intuitivo a preguntas como la planteada y tener en cuenta el conocimiento previo. En lugar de «intervalo de confianza» se calcula el «intervalo de credibilidad», que es la franja en la que se encuentra, con un 95% de probabilidades, por ejemplo, el verdadero valor poblacional.
Fundamentada en el teorema de Bayes, este tipo de estadística utiliza una probabilidad previa y, junto con el experimento o la observación, calcula una probabilidad a posteriori. Esto haría que no se viera cada estudio como algo separado o independiente del conocimiento previo, sino que añadiría nueva información y contribuiría a la creación de nuevo conocimiento, que sería el punto de partida de los siguientes trabajos2.
Leyendo este artículo1, se recuerda la publicación de Gutiérrez-Fisac et al4. en 2012, cuyo objetivo también era conocer la prevalencia de obesidad en España estudiando a 12.883 individuos. Según los datos aportados, la prevalencia de obesidad en su muestra entre 18 y 64 años fue del 19,78%. La estadística bayesiana permitiría utilizar esto como información previa para posteriormente conseguir un conocimiento más profundo calculando el intervalo de credibilidad.
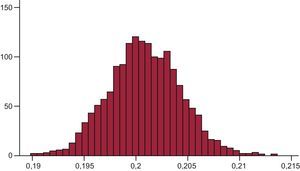
Así, por ejemplo, utilizando como probabilidad de obesidad a priori una distribución beta (1.898,7700)4, la variable obesidad, una distribución de Bernoulli y juntando los datos obtenidos por Aranceta-Bartrina et al1., después de 12.500 iteraciones y un periodo burn–in de 2.500, se obtendría una prevalencia de obesidad a posteriori del 20,1%, con un intervalo de credibilidad del 95% (19,4-20,8%). Es decir, esta vez sí habría un 95% de posibilidades de que la prevalencia general de obesidad en España se encontrara entre el 19,4 y el 20,8%. La figura representa en forma de histograma la distribución de la obesidad según las simulaciones Markov Chain Monte Carlo.
Como se ve, coincide con bastante exactitud con el intervalo de confianza aportado por Aranceta-Bartrina et al1. (19-24,2%), ya que cuando hay poca variación entre los estudios el intervalo de confianza y el de credibilidad se asemejan2. Sin embargo, podría no haber sido así y, si no se utiliza estadística bayesiana, habría 2 opciones: considerar solamente 1 de los trabajos y cerrar los ojos al otro (aun considerando que la metodología de ambos sea correcta) o realizar un tercero que genere mayor evidencia y «desempate», incluso a sabiendas de que ni siquiera responde a nuestra pregunta inicial.