It is well known that cardiovascular function is characterized by, among other factors, a number of biomechanical indices and parameters, and in turn, depends upon the phenomena that they describe. The article by Bia et al1 published in this issue of Revista Española de Cardiología assesses these parameters using in vitro techniques, and concludes that they may be of use in the early characterization of degenerative arterial disease. A number of studies have addressed the influence of mechanical parameters at various levels of the cardiovascular system.2-7 Likewise, some clinical studies have highlighted a need for new hemodynamic indices, which can come from an accurate interpretation of the biomechanics.8
The aim of this short commentary is to define and draw attention to the usefulness of some of these parameters, as well as to establish their limitations in terms of clinical applications and basic research. It is worth noting that the purpose of a precise characterization of these biomechanical terms is not the use of complex formulas or mathematical models, but rather to characterize the real response of the arteries in the most simple and realistic way.
Mechanical factors can be established at various levels:
-Global and regional systemic levels: analyzing, for example, the Windkessel effect of high elastic compliance of the proximal aorta, overall flow resistance of the peripheral vasculature, and global pulse wave propagation.
- Local integrated level: using unidimensional models that integrate the arterial section. These models explain the pulse wave velocity (Moens-Korteweg equation) and define elastic parameters such as the pressure-strain (Ep) or pressure-diameter (Epd) moduli, or viscoelastic parameters such as the Vpd, all of which are used in the article1 published in this issue.
- Local point level: using 3-dimensional models that facilitate a point by point analysis of both blood flow and the response of the arterial wall. Here, the basic relationships are formulated between the forces applied to the tissue (stresses) and its unit elongations (strains), described by continuum mechanics, through models such as linear elasticity (Young's modulus E or the Poisson ratio v) or nonlinear elasticity.
- Micromechanical level: analyzing phenomena such as the microstructure of the arterial wall made up of smooth muscle cells and an extracellular matrix of collagen and elastin, the cellular mechanics (eg, for the endothelial cells) or even the molecular mechanics of the protein chains that form the microstructure of the connective tissue.
Models exist for all of these levels and it is possible to measure mechanical parameters as well as establish correlations with cardiovascular function2,3 and the occurrence or risk of abnormalities.4
Despite the fact that detailed mathematical analysis of biomechanics and hemodynamics may appear novel or recent, all of the basic phenomena mentioned here are well described, not only in the classic biomechanics texts of Fung,9-11 but also in those on hemodynamics.12 Furthermore, many of the phenomena were studied and characterized tens or hundreds of years ago, in some cases even in the 18th century: the Windkessel effect was described by Hales in 173313 and more precisely characterized by O. Frank in 189914; pulse wave velocity was characterized by Young in 180815 and popularized somewhat later by Moens16 and Korteweg.17 Young also developed the elastic modulus of the same name (E). Finally, linear viscoelastic models such as the Kelvin-Voigt model were formulated by Boltzmann in 187618 and applied to the arteries by Hardung.19 It is also noteworthy that the majority of this work was developed in the field of medicine, to which many of the aforementioned authors belonged, and not in more abstract or technical areas such as mathematics or engineering.
In spite of this, more basic research is needed in order to improve our understanding of the properties of blood flow and the response of the arterial tissue at the various levels mentioned above. This research is based on new experimental techniques, mathematical models and computer simulations,20,21 or else on new imaging and image analysis methods.22,23 Likewise, deeper understanding can and should translate into clinical applications in the analysis, treatment and prevention of disease.
The article by Bia et al1 published in this issue describes an interesting study in which they characterize the local mechanical properties for various arterial regions at the level of the arterial section. To this end, they perform in vitro measurements in sheep using a rigorous procedure under pulse-flow conditions similar to those seen physiologically. Characterization of the arterial elastic modulus and wall buffering (WBF), performed with muscle tone, allowed confirmation of known phenomena of the systemic circulation, such as the greater flexibility of the proximal aorta compared with the peripheral arteries (Windkessel effect). In addition, they obtain other interesting results such as the constancy of the viscoelastic time constant (τ=WBF). This study yields results that could be useful in the characterization of pathological deviations or anomalies, or of factors that present cardiovascular risk.
REVIEW OF CONCEPTS AND NOMENCLATURE
In the article by Bia et al,1 and more generally in biomechanics, various technical concepts are employed that may not be in common use in clinical settings. Consequently, it may be helpful to remind ourselves of their precise meaning or even the correct nomenclature in Spanish (incorrect, ad hoc translations of English terms are often generated, generating confusion). In an effort to offer a consistent terminology, the following section offers--without pretense of originality--a review that may be useful for the study of biomechanical indices in hemodynamics. A more detailed description can be found in specific articles.9,10,12
Stresses, Strains, and Elastic Moduli
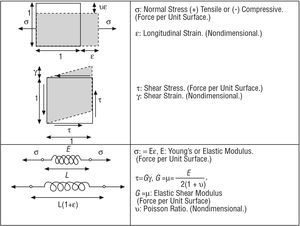
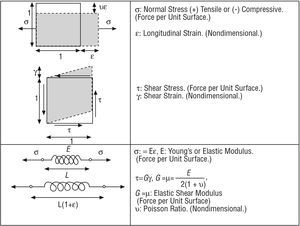
The mechanical forces on a tissue are characterized using the concept of stress (force per unit surface), which causes strain in various directions. Essentially, stresses and strains are related by the elastic modulus (Figure 1).
Figure 1. Stresses, strains, and elastic moduli.
Parameters of the Arterial Section
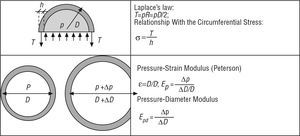
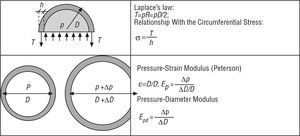
The concepts described above allow the response of the arterial section to be determined through the use of simple models integrated in this section (Figure 2).
Figure 2. Arterial section models.
Models That Define the Behavior of the Arterial Wall: Linear and Nonlinear Elasticity
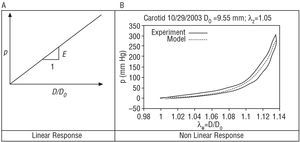
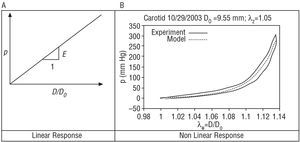
In the following section, the mechanical response that an artery would have to variations in blood pressure according to the ideal hypothesis of a linear elastic tissue is compared with the real response, which is neither linear nor perfectly elastic (Figure 3).
Figure 3. Elasticity models.
A tissue showing perfectly linear elastic behavior (Figure 3A) is characterized, across its strain range, by a single modulus of elasticity (slope of the response curve), with a single arm for load and unload.
However, soft tissues of the human body are highly nonlinear, and their response is not perfectly elastic. Consequently, it is not possible to establish a unique modulus of elasticity. Instead, it must be evaluated incrementally at each point, using a tangent (for small pressure perturbations) or a secant to the response curve of the material (eg, between the diastolic and systolic pressure). Figure 3B shows the result of an in vitro assay using healthy human carotid (performed by G. Guinea et al in the Department of Materials Science, Universidad Politécnica de Madrid [personal communication]). The assay reveals a first phase for low pressures in which the artery is more flexible and the mechanical response is mainly due to elastin. When the pressure is increased, a strong increase in rigidity occurs due to collagen fibers being placed under stress. This natural mechanism of rigidification, common to the majority of soft tissues, endows stability and guards against damage, preventing excessive strains that would rupture the tissue. On the other hand, although the assay was performed at a slow rate, a clear difference is seen between the loading and unloading arms, indicating that the tissue does not respond exactly according to an elastic model. A nonlinear elastic analytic model (in green) has been adjusted in order to allow a computer simulation using finite elements of the tissue.20 The authors of the study published in this issue1 characterize the different elastic moduli used via a secant or a tangent, depending on the particular case.
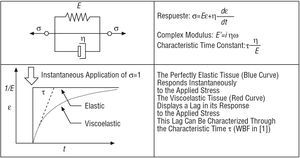
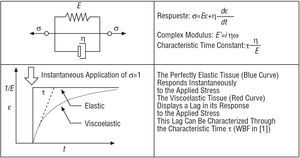
Viscoelasticity
Finally, a brief review is provided below of the most elementary viscoelastic model, designated Kelvin-Voigt, which is also used by the authors in the paper to which this editorial refers.1 Viscoelasticity leads to a retarded response compared with the elastic response, which would, in theory, be instantaneous. The Kelvin-Voigt model has various limitations, such as the fact that it predicts a hysteresis that is dependent upon the frequency.12 However, it can be adequate for characterization at a single frequency, such as that used by Bia et al1 (Figure 4).
Figure 4. Viscoelastic model..
OTHER POTENTIAL LINES OF INVESTIGATION
As mentioned, there still exist numerous limitations to our understanding of cardiovascular biomechanics and hemodynamics. It should be remembered that tissues exhibit complex characteristics that must be taken into account in order to achieve realistic interpretations. Such characteristics include nonlinear elasticity, anisotropy, viscoelasticity, and poroelasticity, as well as the need to determine properties through realistic in vitro experiments confirmed by in vivo measurements. Likewise, analyses are required on different scales, such as the cellular mechanics of the endothelium. It is not viable to generate a single mathematical model or simulation that incorporates all of the phenomena mentioned; consequently, it is necessary to base decisions on the specific application.
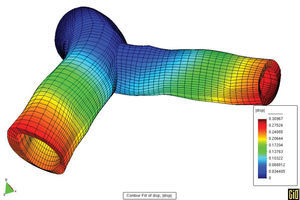
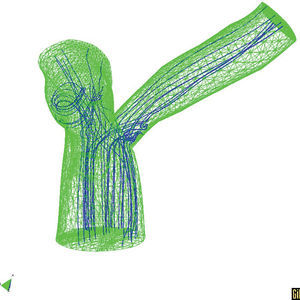
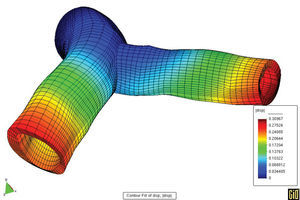
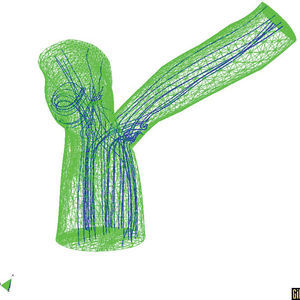
We should take advantage of the technological and scientific advances in experimental equipment and imaging techniques, along with mathematical and numerical models and their application in computer simulation. In light of this, it is worth mentioning the techniques in fluid dynamics that allow precise determination of local, three-dimensional hemodynamic effects. Likewise, finite elements methods can offer precise information about the mechanobiological state and progression of arterial tissue. As an example of this type of model, Figures 5 and 6 show the results of a coupled simulation of the blood flow and the strain on the arterial wall in the left coronary artery,24 the geometry of which has been reconstructed using modern in vivo cardiovascular imaging techniques and computational geometry.
Figure 5. Parallel simulation of flow and strain on the arterial wall.
Figure 6. Three-dimensional T model with the predicted the trajectory of the particles.
CONCLUSION
As Bia et al1 remind us, mechanical alterations are one of the earliest manifestations of degenerative arterial disease. Sufficient understanding of these phenomena and their detailed study will facilitate the detection, treatment, and monitoring of their effects on the cardiovascular system, with the consequent health benefits that this implies.
Correspondence: Dr. J.M. Goicolea Ruigómez.
Grupo de Mecánica Computacional. Universidad Politécnica de Madrid.
Prof. Aranguren, s/n. Ciudad Universitaria. 28040 Madrid. España.
E-mail: goico@mecanica.upm.es