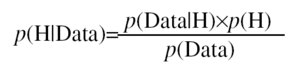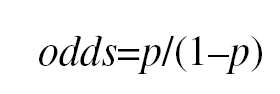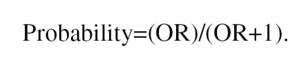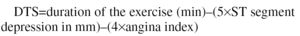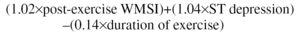The word "imaging" easily relates to the diagnosis of heart disease, but not to prognosis. In quality of life questionnaires, the most frequent responses from patients to the question "What do you expect after visiting the physician?" are: to live for as long as possible, be able to carry on with their daily activities, be free from symptoms and side effects from the treatment, and to continue working. These replies can be summed up by the variables mortality, morbidity, and disability, which basically relate to prognosis. In the case of ischemic heart disease, evaluating the prognosis means assessing the risk of adverse events, such as death of cardiovascular origin, myocardial infarction, unstable angina, revascularization procedures, and heart transplant. Risk can be defined as the probability that an adverse event will occur, which, defined non-mathematically, is the evidence-based degree of confidence of this event occurring. In fact, this is an ongoing process by which the cardiologist adjusts his/her level of confidence whenever the patient provides him/her with new evidence in favor of or against the presence of coronary artery disease. The signs or tests are analyzed via the mathematical theory of conditional probabilities or Bayes theorem. In our case, we would have a set of variables derived from the medical record, physical examination, electrocardiogram, bidimensional echocardiogram, and treadmill exercise stress test which determine the pre-test probability (p[H]). This probability--or confidence level--will be modified by the results of exercise echocardiography (p[Data]) and will eventually become the post-test probability (p [H|Data]) via the following equation:
Risk assessment can be expressed as categories, e.g., risk of death from cardiovascular disease can be established as low (<1% per year), medium (1%-5% per year) and high (>5% per year). This is important because these categories can provide a guide for the cardiologist (low risk: medical discharge; medium risk: new assessments; high risk: intervention). No test can be analyzed in isolation without taking into account the basic information provided by the medical record, physical examination, and previous tests.
Converting raw clinical data into a tool to predict events involves the use of complex mathematical techniques, such as logistic regression analysis. The fundamental aim of this technique is to model how the presence or absence of several variables and their value or level influences the probability of a normally dichotomous event occurring. Variables with discriminant power are used to construct algorithms that make it possible to estimate the probability of the event (e.g., mortality). One of the interesting characteristics of logistic regression is its relationship with a parameter for quantifying risk known as the odds ratio (OR). The odds of an event is defined as the ratio between the probability of it taking place versus the probability of it not taking place:
where p is the probability of the event. Thus, for example, the mortality odds ratio for left ventricle wall movement abnormalities (WMA) during exercise echocardiography testing (EE) determines how many times it is more probable that death occurs during patient follow-up than not, when WMA is present. In addition, we could calculate the mortality odds ratio when no WMA is present under EE. If we divide the first odds by the second one, we have calculated the odds ratio (OR) which, in some ways, quantifies how much more probable a future death is when presenting WMA (first odds) than when not. The concept behind this measurement is similar to that of relative risk (RR), which refers to the probability ratio that an event (death) occurs when WMA is present versus when it is not. The proportional hazards model, or Cox's model, is a type of regression analyses for specifically calculating the survival rate--free from events--as a function of time and prognostic variables, and uses the hazard ratio (HR) as a related measurement. When the OR, RR or HR are >1 there is a risk factor. In contrast, an OR, RR or HR <1 indicates a protective factor. The OR can be converted into a probabilityor riskthrough the formula:
Combining clinical variables with ST segment response during exercise improves the usefulness of the treadmill exercise stress test to assess prognosis in the coronary patient. Many authors have derived simple equations from complex regression studies that demonstrate the foregoing. Of these, the Duke scale is the most often used (Duke Treadmill Score [DTS]).1 This scale uses the duration of the exercise in minutes, the depth of ST segment depression in millimeters, and an angina index with value 0 when the symptom is not present, and 2 or 1 according to whether limits occur during the exercise or not. The formula is as follows:
In this scale--which can have negative values--a score of less than -10 places the patient in a high-risk category, between -10 and +4 in an medium-risk category, and more than +5 in a low-risk category. Carrying out additional explorations, such as EE, is not justified in a low-risk patient without angina, according to the Duke scale. These patients have low mortality due to cardiovascular causes during follow-up and EE does not offer additional information.2 However, several researchers have shown that imaging is better than an electrocardiogram as a source of information relating to prognosis in patients with medium risk.3-5 Nuclear techniques (Single Photon Emission Computed Tomography [SPECT]) and EE, that evaluate perfusion and left ventricle contractile function, respectively, have similar diagnostic precision6 and are better than clinical variables, standard exercise stress test and resting echocardiogram in predicting events, especially infarctions, hospitalizations due to unstable angina, and death of cardiovascular origin. However, when SPECT and EE are compared they offer similar prognostic value.4 One study applied the two techniques at the same time to 248 patients with known or suspected coronary disease and were monitored for 3.7±2 years. It was shown that risk of death was 3.95 times greater per unit increment in the post-exercise wall motion score index (WMSI) and 1.41 times greater per each 10% increment in perfusion defects with thallium. Imaging (WMSI via EE or perfusion defect via SPECT) was the only independent predictor of death in these patients.4 Another study by the same group of researchers presented an equation derived from a multivariate analysis that included EE and standard exercise stress test carried out in 388 patients with known or suspected coronary disease. The algorithm was basically a reformulation of the one proposed by Duke's group:
where post-exercise WMSI replaced angina as a predictor variable. Subsequently, the formula was applied to another group of 105 patients who were monitored prospectively for 3 years. This new index succeeded in appropriately stratifying event risk into 3 groups: high (29.6% events), medium (19%-15% events), and low (no events during 3-year follow-up) with values in the upper quartile (+0.66 to +2.02) for high-risk patients, and in the lower quartile (-1.22 to -0.47) for low-risk patients. The OR of this new indicator is 2.94/unit (95% confidence interval [CI], 1.4-6.2; P=.0043).5 Two aspects of this new algorithm should be emphasized. The first is that, in the ischemic cascade, wall movement changes precede angina, which explains the substitution of the angina index by the post-exercise WMSI in the new formula, despite the known value of the symptom in evaluating the diagnosis and prognosis of patients with coronary disease. The second is that the coefficient multiplied by the ST segment depression is much smaller than in Duke's algorithm, given that the electrocardiogram is less relevant when imaging of the heart during exercise is done at the same time.
The study by Peteiro Vázquez et al7 demonstrated the superiority of EE in determining prognosis compared to clinical variables, exercise stress testing, and resting echocardiography in a technically challenging circumstance, as presented by image capture during maximum exercise. This study confirmed that imaging is better than the electrocardiogram in predicting cardiovascular events, especially death. The predictor variables are similar to those found by other researchers and are related to the ability to carry out exercise and the presence and extent of ischemia/necrosis. However, the logistic model finally includes clinical and resting echocardiography variables, which demonstrates the importance of information regarding pretest probability. The survival analysis done in this study shows that a WMSI<1.5 at the moment of maximum exercise involves a low risk of events. Previously, a very similar cut-off point (WMSI 1.4) has been demonstrated through imaging done immediately post-exercise, which has been associated with approximately 15% of perfusion defects via SPECT. Patients with abnormal findings, but with a WMSI below this cut-off point could benefit more from aggressive medical treatment than from an invasive therapeutic strategy. This was demonstrated in a study which explored the relationship between the extent and severity of the ischemia and survival after revascularization.8 In this study, SPECT was done in 10 627 patients without previous infarction or intervention with a 2-year follow-up. During this period 146 patients died (1.4%). Multivariate analysis, based on the Cox model, demonstrated greater survival in the patients who received medical therapy when SPECT showed no or mild ischemia. In addition, revascularization benefited the patients with moderate to severe ischemia (>10% perfusion defect). This article also demonstrated the importance of estimating risk as a threshold for therapeutic decision-making.
The work of Castillo Moreno et al9 evaluated the use of dobutamine stress echocardiography (DSE) in patients with stable angina, without significant changes in baseline electrocardiogram, without a background of revascularization, and with a low rate of previous infarctions and good left ventricular function; that is, a group of patients in which all the guidelines would recommend carrying out a standard exercise stress test to stratify risk. However, in symptomatic patients, EE has demonstrated that it can contribute additional information to prognosis.2 The study confirms the validity of the Duke scale but, at the same time, it demonstrates the additional contribution of DSE. The authors recognize that EE is the first option to standard exercise stress testing in patients who can perform the exercise. They also pointed out that their study did not try to evaluate what modality of stress would be more suitable or best indicated but attempted to find out to what extent SDE independently contributes to identifying patients with a high risk of events and facilitate decision-making. They rightly conclude that using risk stratification models based on several variables makes it possible to integrate all the information available prior to a test and improve its predictive performance. Given that the demonstration of ischemia via imaging contributes additional information to the prognosis of the patient, it is worth questioning whether the technique used to induce ischemia (exercise or drugs) or the method used for its visualization (ultrasound, radioactive isotopes, or magnetic resonance) really matters. Other conditions, such as availability, experience with the technique, safety, and costs frequently override the guidelines. In Latin America, for example, two-thirds of the articles published on stress echocardiography during 1997-2002 are dobutamine studies.10
After searching for a reference method for predicting prognosis in patients with coronary disease we could find ourselves facing the following fact: the best test is to integrate all the tests. This type of mathematical strategy, called consensus algorithm,11 is used in other disciplines, such as space engineering. The percentage of correctly stratified patients increased from 67% with only the exercise stress test to 77% when algorithms derived from multivariate analyses were used, and then to 90% when consensus algorithms were applied. The integration of several algorithms requires mathematical programs that could be carried in modern cardiologists' pocket computers. The expert physician intuitively uses a theorem postulated by the priest Bayes 3 centuries ago, which relates the concepts of sensitivity, specificity and prevalence to post-test probability. Could such expertise be transferred to a pocket computer? It is likely that it could. Could the computer replace the cardiologist to an advantage? Fortunately, the reply is no: the physician and the computer together make the best team.11
See Articles on Pages 916-23 and 924-33
Correspondence: Dr. L. Olmos.
Servicio de Cardiología. Policlínica Portuguesa.
Calle 24 entre Avda. 32 y 33. Acarigua 3301. Portuguesa. Venezuela.