There are large groups of cardiological patients with no strong evidence base to guide medical actions. Recently, the difficulty of clinical decision-making has increased considerably due to several factors such as the increase in life expectancy and comorbidities, the lack of evidence derived from clinical trials in certain subgroups, or respect for patient preferences.

Heart team decision-making1 has arisen in response to the challenge of complex cases and has received the strongest recommendations. However, this system of decision-making has not been scientifically evaluated.

It is very difficult to conduct specific experiments to identify errors in clinical decision-making, and therefore the epistemological basis supporting heart team decision-making is weak. However, this barrier can be crossed with the methodological tools of social sciences that have already been used to study group decision-making in other fields such as business or electoral systems. The aim of this article was to assess heart team decision-making from the perspective of social sciences.

Study of the aggregation of individual preferences is important because in many human activities, decisions are collectively taken. Nicolas de Condorcet, an eighteenth-century French mathematician and revolutionary, pioneered the application of probability theory to collective decision-making. One of his objectives was to mathematically substantiate decision-making in democratic systems, which began to be instituted in the late eighteenth century.

Condorcet's Jury Theorem2 concluded that if each member of a jury is more likely than not to make a correct decision, the probability that the highest vote of the jury is the correct decision increases as the number of members of the jury increases. This theorem also states that if there are only 2 options, the overall preferences of a group are consistent with the preferences of the majority of its members. Therefore, heart team decision-making has emerged as an attractive tool for decision-making in complex patients.

However, when there are more than 2 options, the general preference of a group cannot match the preferences of its members3; this might occur, for example, in a heart team deciding on the best treatment for a patient with multivessel coronary disease when the choice is between medical management, coronary surgery, or percutaneous coronary intervention. This is mainly caused by 2 paradoxes:

• •

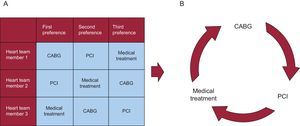
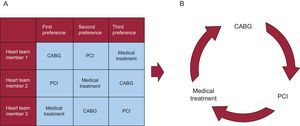
  Condorcet's Paradox.3 In voting systems, when there are more than 2 options and more than 2 voting members, the sum of individual preferences can generate an order of general preference leading to a vicious circle in which the group expresses a preference for A over B, a preference for B over C, and a preference for C over A. This can sometimes lead to the choice of a global preference that does not match the aggregation of individual preferences (Figure 1).

  
  

  Figure 1.

  A: Example of preferences matrix of the heart team for patients with multivessel coronary disease. B: Condorcet's paradox showing that collective preferences can be cyclic (intransitive), even if individual preferences are not cyclic. CABG, coronary artery bypass graft; PCI, percutaneous coronary intervention.

  (0.15MB).
• •

  Arrow's Paradox or Impossibility Theorem.4 If there are more than 2 alternatives and 2 voting members, Kenneth Arrow (Nobel Prize in Economics) mathematically demonstrated that no collective decision rule meets all the following rational criteria, unless a person has a leadership position allowing that person to impose his or her own preferences (the dictatorship). The rational criteria are:

  • -

    Universality or Unrestricted Domain: Individuals may switch their order of preferences without restrictions. Any order among the alternatives is possible.

  • -

    Unanimity or Pareto Efficiency: If all the members of a group prefer A over B, then A is above B in the list of overall preferences.

  • -

    Monotony: If a method of choice means that A is above B in the list of overall preferences and a member who prefers B over A changes his or her preference, the method must maintain A above B in the preferences list.

  • -

    Independence of irrelevant alternatives: If there are 2 alternatives, A and B, for which the method of choice means that A is preferred to B, when members change their preferences regarding other alternatives to A and B, the method continues to maintain that A is preferred to B. Therefore, the position of other alternatives in the preferences list is irrelevant to decide the relative order of A regarding B.

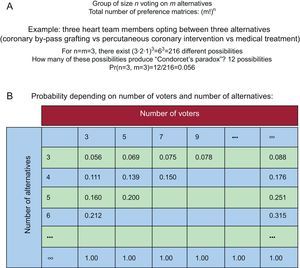
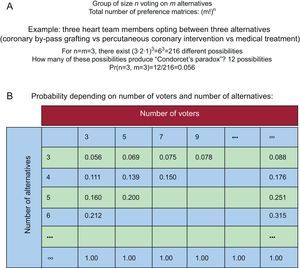
Initial studies of Condorcet confirm that heart team decision-making for dichotomous choices is superior to individual decisions. However, when the range of options is more than 2, heart team decision-making can present defects and not accurately reflect the preferences of its members. Fortunately, these paradoxical cycles rarely occur in medicine, where there are usually few alternatives. By contrast, in other social fields it can be very limiting because there are frequently many alternatives5 (Figure 2).

Figure 2.

Probability of paradoxical cycles (Condorcet's paradoxes). Modified with permission from Riker.5

(0.29MB).

Nevertheless, the main usefulness of the heart team is to reach the best solution for a specific case, depending on patient characteristics (age, comorbidities, extent of cardiovascular disease...) and local experience, including discussion with other specialists, such as nephrologists or anesthesiologists. Heart team members must interact to reach agreement on the best solution for each patient, with respect for patient preferences, not just voting.

Our article shows that heart team decisions can sometimes be paradoxical, but this could be mitigated through multidisciplinary discussion, assessing the patient's characteristics and the institution's results for each disease.