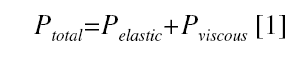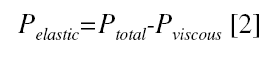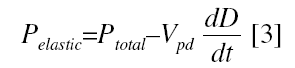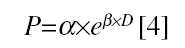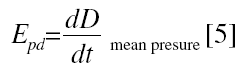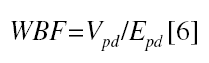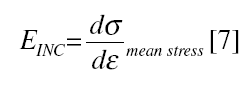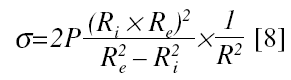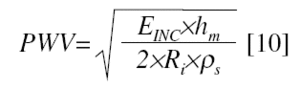Keywords
INTRODUCTION
The viscoelastic properties of the great arteries determine their main functions: to conduct blood (conductive function) and to buffer the pulse pressure and flow generated by ventricular ejection (wall buffering function, WBF).1,2 Various diseases that affect arterial viscoelasticity have a diffuse presentation with affected and healthy segments interspersed.3 Consequently, "global" or "regional" indices of arterial function (eg, total compliance) are unable to detect early-stage vascular disorders.3,4 In addition, the incidence, severity, and predominance of a given vascular condition (eg, arteriosclerosis) differs according to the location of the segment under consideration in the arterial tree.5 This observation has been linked to differences in the viscoelastic properties of the different arteries.5 The diffuse nature and regional differences in vascular conditions have led to an increasing interest in identifying biomechanical differences between systemic arteries and undertaking clinical evaluations of the "local" function of individual segments.5 To this end, systems have begun to be used that allow the instantaneous arterial pressure-diameter relationship to be monitored.6,7
In general, the elastic and viscous properties of the arterial wall have been characterized together as "viscoelasticity."8 Various studies have demonstrated that the elasticity and viscosity of the arterial wall play different roles in arterial function,1,2 and can also be independently affected by physiologic, pathologic or experimental conditions.1,2,6,7,9,10 Consequently, adequate evaluation of local arterial function requires separate characterization of the elastic and viscous responses, and with them the WBF. In light of this, we have recently proposed the determination of WBF through the relationship between the arterial viscous and elastic moduli.1,2,9
In general, the viscous response has not been considered when evaluating arterial function. This is mainly due to methodological difficulties; the nonlinear character of the arterial pressure-diameter relationship is the principal limitation to the determination of the response in the frequency domain.8,9,11 To characterize it, we have used a series of procedures in the time domain that were originally proposed by Bauer.12 Using these procedures, the nonlinear character of the pressure-diameter relationship does not present significant difficulties.1,2,13
The dependence of the elastic and viscous responses on mean and pulse pressures and stimulation frequency, among other factors, means that to compare the viscous and elastic moduli of different arterial segments, they must be analyzed under identical experimental conditions, including those of the normal work of each segment. Although it has been suggested that the arterial viscoelastic response displays regional differences,8,11 to our knowledge there have been no studies in which such differences have been characterized using dynamic, isobaric analyses, which analyze the instantaneous pressure and diameter signals in the time domain and characterize viscosity and elasticity separately. Likewise, we are unaware of any study in which possible differences in the local WBF have been assessed.
The aim of this study was to characterize the regional differences in the elastic and viscous responses of the arterial wall, and in the WBF of the central and peripheral systemic arteries using dynamic and isobaric analysis of the arterial pressure-diameter relationship in the time domain. In addition, the intrinsic elastic response of the artery was quantified using parameters that allowed its rigidity to be characterized independently of the arterial dimension.
MATERIALS AND METHODS
Surgical Preparation
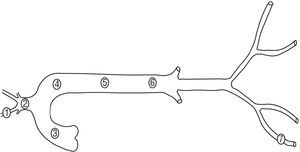
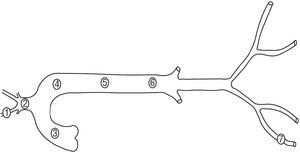
Six Merino sheep (35 kg to 45 kg) were anesthetized with intravenous sodium pentobarbital (35 mg/kg). The neurovascular bundle of the neck and right hind limb were dissected and bilateral thoracotomy was performed. Segments (5 cm long; marked by adventitious sutures) were dissected from the right carotid artery, the brachiocephalic trunk, the right femoral artery, the ascending thoracic aorta, and the proximal, medial, and distal descending thoracic aorta (Figure 1). A pressure microtransducer (Konigsberg Instruments Inc., Pasadena, USA), calibrated at 37°C using a mercury manometer, was introduced into each segment. A pair of ultrasound crystals (5 MHz, 2 mm diameter) were sutured to the adventitia in diametrically opposed sites and connected to a sonomicrometer (Triton Technology Inc., San Diego, USA). The transit time of the signal between the crystals (ultrasound velocity: 1580 m/s) allowed the instantaneous diameter of the segment to be calculated.1,2 Following instrumentation, the selected arterial segments were excised with the sensors located in their medial portion. Finally, the animals were sacrificed by pentobarbital overdose and intracardiac administration of potassium chloride. All procedures were performed in accordance with international guidelines.14 The methods used had been employed previously by our group.1,2,9,13,15
Figure 1. Arterial segments studied. 1 indicates the carotid artery; 2, the brachiocephalic trunk; 3, the ascending aorta; 4, the proximal descending thoracic aorta; 5, the medial descending thoracic aorta; 6, the distal descending thoracic aorta, and 7, the femoral artery.
In Vitro Studies
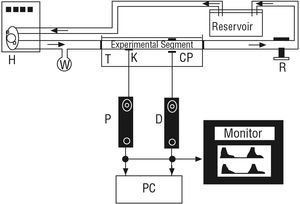
The excised arterial segments were mounted in an in vitro perfusion system15 (Figure 2) made up of polyethylene tubing, a tubular resistance regulator, a reservoir containing Tyrode's solution, and an artificial heart (Jarvik Model 5, Kolff Medical Inc., Salt Lake City, USA) fed by a pneumatic electric pump.15 The arterial segments were mounted in a gap in the tubing and the ends were attached to the tubes using ligatures, thereby closing the system and allowing circulation of oxygenated Tyrode's solution at 37°C, pH 7.40. The arterial segments were studied at the same length as in vivo. Thus, when they were mounted in vitro, they were extended; the average extension ratio (λ = length in vivo/excised length) was 1.25. The mounted segment was immersed in Tyrode's solution. The pulse-pressure range and pumping frequency were regulated by the pump controls, while altering the resistance and reservoir height allowed the mean pressure and the form of the pressure waves to be controlled. After mounting the segment, it was left for 10 minutes under conditions of stable pressure, flow, and pumping frequency prior to beginning measurements. During this period, the diameter signal was calibrated in millimeters using the calibration system of the sonomicrometer.1,2,9,13
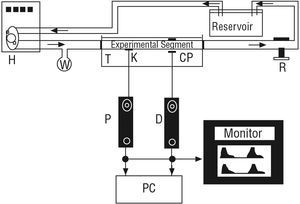
Figure 2. In vitro system. H indicates pneumatic pump and artificial heart; K, pressure sensor (Konigsberg); CP, diameter sensor (ceramic piezoelectric); P, pressure signal; D, diameter signal, and PC, computer. Arrows indicate the direction of flow. T, container filled with Tyrode's solution. Reservoir contains Tyrode's solution. W indicates a distensible chamber. R indicates a flow resistor.
Experimental Protocol
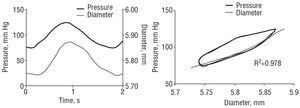
The diameter and pressure of each segment was determined and stored during a single stable period. The pumping frequency was similar to the cardiac frequency of the sheep.1,2 The segments were subjected to pressure pulses that were similar in shape and magnitude to those observed for the systemic circuit under physiological conditions (Figure 3). At the end of the experiment, the segments were weighed.
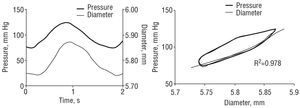
Figure 3. Left: femoral pressure and diameter signals. Right: femoral pressure-diameter relationship. Black lines indicate the total pressure-diameter relationship. Gray lines indicate the pure elastic pressure-diameter relationship, obtained after minimizing the area of hysteresis for calculation of the viscous modulus. Note the exponential adjustment to the pure elastic relation.
Data Collection and Analysis
The diameter and pressure signals were visualized in real time and digitized (sampling frequency of 200 Hz). For each segment, 20 to 30 consecutive beats were stored.
Quantification of the Elastic and Viscous Response
Representation of the arterial wall through a Kelvin-Voigt viscoelastic model allowed the pressure-diameter elastic modulus (Epd) and the pressure-diameter viscous modulus (Vpd) to be calculated.1,2,9 The model considers the pressure exerted on the wall to be distributed in terms of an element representative of the wall elasticity (spring) and another that is representative of the wall viscosity (buffer).1,2,16 The total observed pressure can be separated into elastic and viscous components:
Reordering equation [1] we obtain
The Pviscous is proportional to the first derivative of the diameter with respect to time1,2,9,13:
where Vpd is the wall viscous modulus and dD/dt is the first derivative of the diameter with respect to time. An arterial pressure-diameter relation was constructed from the temporal signals of pressure and diameter for each pulse to be analyzed.1,2 For each pulse, the area of hysteresis of the pressure-diameter relation was reduced via an incremental-iterative computational procedure for the value of Vpd in equation [3].1,2 Once the minimum area was obtained, the incremental-iterative procedure was stopped and the value of Vpd was considered equivalent to the viscous modulus.1,2 Then, an exponential function was adjusted to the resulting pure elastic pressure-diameter relation, obtained upon elimination of the area of hysteresis (Figure 3)1,2:
The Epd was calculated as the slope of the function at the mean diastolic pressure1,2:
Wall Buffering Function
Using a Kelvin-Voigt model, the capacity of the arterial wall to buffer a pressure stimulus emerges from the relationship between the pressure stimulus and the resulting strain.1,2 As in previous studies,1,2 the WBF was quantified as
The lower the WBF, the lower the buffering capacity of the arterial wall.1,2
Quantification of the Elastic Response: Parameters Independent of the Diameter
In order to compare the results obtained for elastic response with those from the literature, and to assess the regional differences in arterial rigidity independent of arterial dimensions, we calculated the incremental Young's modulus (EINC) and the clinical indicators pulse wave velocity and the pressure-strain elastic modulus (Ep).
To calculate the EINC, the arterial stress-strain relationship was constructed for each pulse to be analyzed.13,16 Using a similar procedure to that described earlier, the area of hysteresis was eliminated and a pure elastic stress-strain relation was obtained.13 The EINC was then calculated as
where dσ and dε are the first derivatives with respect to time of the circumferential stress and the arterial strain in the pure elastic relation, respectively.16 The EINC is always calculated for the dσ/dε corresponding to the mean diastolic stress. The following equation was used to calculate σ13:
where P is pressure, Ri is the internal arterial radius, Re is the external arterial radius, and R is the mean arterial radius (R=[Ri+Re]/2).13 The strain (ε) was calculated13 as
where R0 is the arterial radius at a pressure of 0 mm Hg. The pulse wave velocity was calculated16 as
where hm is the mean wall thickness13 and ρs is the blood density (ρs=1.06 g/mL). The Ep was calculated16 as
where PS and PD are systolic pressure and diastolic pressure, respectively, and DS and DD are systolic diameter and diastolic diameter, respectively.
Statistics
For each arterial segment, the values of the hemodynamic and biomechanical parameters represent the mean of 20-30 beats. The values calculated for each artery type are expressed as the mean (SD). The presence of significant differences between the groups was assessed by ANOVA followed by the Bonferroni test. Statistical significance was set at P<.05.
RESULTS
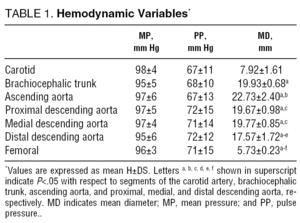
Table 1 shows the hemodynamic stimulation variables and the mean diameter of each segment. Note that the segments were stimulated with similar pressure levels (isobaric studies), stimulation frequency (isofrequency studies), and using pressure waves similar to those encountered under physiological conditions (Figure 3). The use of isobaric comparisons ensured that differences observed in rigidity were not due to differences in the distension pressure. The use of isofrequency comparisons ensured that the differences seen between Vpd values were not due to differences in the wall stimulation velocity. Finally, note that the mean diameter decreased as the arteries became more peripheral.
Table 2 shows the mean values for the Epd and Vpd moduli and the WBF for each group of segments. Note that the Epd and Vpd were higher the more peripheral the segment. This indicates that the arterial rigidity and the viscous response of the wall increase towards the periphery. Note also the slight increase in the Epd and the Vpd between the ascending aortic and the proximal and medial descending aortic segments, and the sharp increase in the distal descending aortic, carotid, and femoral segments. In addition, observe that, despite the variation in the Epd and Vpd between the differen t segments, the WBF did not show significant differences.
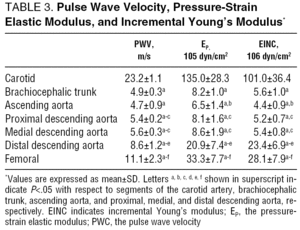
Table 3 shows the pulse wave velocity, the EINC, and the EP. The values obtained for these parameters are consistent with those seen in the literature.16 Note that the pulse wave velocity and both elastic moduli increase towards the periphery. However, when using these parameters, which take into account the arterial geometry, the differences in the elastic response of the segments were lower than those found when using the Epd modulus (Table 2). The reduction did not alter the tendency of the elastic response to increase towards the periphery. However, it did mean that the differences in the EINC and EP seen between the brachiocephalic trunk and medial descending aorta were no longer statistically significant.
DISCUSSION
Th e following discussion is focused on the 2 main findings from the study: a) the elastic and viscous response of the arteries, obtained f rom a time-series analysis of the arterial pressure-diameter relationship, increased towards the periphery, and b) despite the variation in the elastic and viscous response, the WBF did not show significant differences between segments.
Elastic and Viscous Response: Regional Differences
Three moduli of elasticity previously defined and used by other authors1,2,7,16 were used to evaluate the elastic response. This allowed comparison of the results obtained here with those found in the literature, as well as serving as a reference for future approaches. Although all of the moduli evaluate arterial rigidity, the different ways in which the calculations are performed generate complementary information relating to the mechanical properties of the arteries.16 The EINC is commonly used in elasticity theory because it best defines the intrinsic properties (independently of the geometry or size) of a given material (eg, the arterial wall).4,16 Consequently, it is considered the "gold standard" for the evaluation of the elastic response of a material.16 The requirement for the geometric characteristics of the arterial segment (thickness and diameter of the arterial wall) to be known makes this a difficult modulus to calculate in a clinical setting.14,16 Due to the nonlinearity of the pure elastic stress-strain relation, calculation of the EINC requires that the stress or strain for which it is calculated is systematized and determined. The calculated Epd modulus can be measured in the clinic based on the signals for the instantaneous arterial pressure and diameter. Like the EINC, the pressure or diameter for which it is calculated must be defined. It allows the arterial rigidity to be evaluated independently of the viscous properties of the arterial wall since it is calculated by eliminating the hysteresis of the pressure-diameter relation. Furthermore, it allows the WBF to be calculated, since it has units that are consistent with the Vpd. Finally, the Ep allows calculation of the arterial rigidity in relation to the unit strain, and as such, is independent of the diameter.16 Its particular clinical usefulness comes from the fact that it is only necessary to know the maximum systolic and minimum diastolic values of the arterial pressure and diameter signals in order to perform the calculation.16 However, since the calculation requires the use of the maximum and minimum values for pressure and diameter in order to calculate the secant between these points, its value includes both the elastic and viscous behavior of the arterial wall. Thus, due to the viscoelastic characteristic of the arterial wall, the maximum systolic diameter of the artery reached during arterial distension is highly dependent upon the level of arterial viscosity.
The elastic response of the artery is an important determinant of its conductive and buffering roles.1,2,9,17-19 An adequate elastic modulus allows systolic distension of the artery and the subsequent diastolic elastic recoil, which ensures the continuity of anterograde blood flow. In addition, an adequate elastic modulus reduces the oscillations generated by the heart,19 minimizing the arterial and ventricular systolic pressure and increasing the arterial diastolic pressure, while ensuring that the mean arterial pressure is high and the pulsatility low.1,2
The relative importance of the elastic response of a segment over the heart, the arteries, and the microcirculation varies according to the site occupied by the segment in the vascular tree. Our data show that the ascending aorta presents the lowest elastic modulus (Tables 2 and 3). This could be related to the fact that it is the only segment that receives the entire ejected volume from the left ventricle, necessitating maximal distension capacity to minimize ventricular afterload. The elastic response tends to increase in more distal segments. However, no significant differences were seen between successive arterial segments from more proximal regions. This gradual increase in the elastic response in the thorax may indicate that these segments contribute to reducing the ventricular afterload and ensuring an adequate systolic arterial reservoir function.
Beyond the distal descending aortic segment, the elastic response of the arterial wall increases sharply, an observation that is in agreement with findings in canine arteries.16 The degree of increase depends on the modulus used to characterize the elastic response. When using pulse wave velocity, EINC, and EP, the differences in elastic response between the peripheral segments, and between these and the central segments are lower than those obtained using the Epd. However, the differences between peripheral and central segments continue to be high, demonstrating that they respond mainly to differences in arterial wall structure. The higher elastic modulus of the peripheral segments may be related to an increase in the fraction of collagen in the arterial wall and to the arterial "radius/thickness" ratio towards the periphery. Under isobaric conditions, the higher radius/thickness ratio would lead to a higher wall tension (Laplace law) in the peripheral arteries,13 compensated by a higher degree of wall rigidity, thereby preventing wall rupture.10,20 In addition, it may indicate that their level of elastic response may be of relatively lesser importance than those of the central arteries for the determination of ventricular afterload.
The viscous response of the arterial wall causes the arterial system in systole to dissipate like heat, part of the energy imparted by the heart in each beat.1,2,13 The viscosity attenuates the highest frequency components of the incident waves of pressure and flow19 and the amplitude of the reflected waves that could trigger resonance phenomena in the system.17 Furthermore, mechanical damage to the arterial wall would be reduced by eliminating the high frequencies that would cause early fatigue.9,19 Thus, the viscosity contributes to the WBF.1,2,19 In contrast to these beneficial functions, Milnor21 postulated a damaging effect of viscosity caused by a 10% to 20% increase in ventricular afterload.
Our results show that wall viscosity, quantified using the Vpd, increases towards the periphery. The lower Vpd of the central arteries, which receive the ventricular ejection directly, could be considered as a "strategy" to minimize ventricular afterload. Given that the viscosity has been correlated with the net amount of smooth muscle cells in the arterial wall,1,9 the higher Vpd of the peripheral arteries, and of the carotid compared with the femoral artery could be explained by higher levels of smooth muscle cells in the peripheral arteries,11,13 and in the carotid with respect to the femoral artery.11 The higher Vpd of the peripheral vessels would lead them to be the most responsible for energy dissipation from the vascular system.
Wall Buffering: Regional Differences
Recently, in anesthetized animals, we found that the local WBF of the ascending aorta and the main pulmonary aorta is similar, despite their differences in elastic and viscous response.1 In both arteries, under conditions of acute hypertension with activation of vascular smooth muscle cells, the WBF remained similar to the basal value, despite the increased pressure dependent upon the Epd. This maintenance of the WBF is due to the increase in the Vpd modulus generated by the muscle activation. Based on these findings, we postulated that the WBF could be considered as an arterial constant that is independent of the hemodynamic circuit, and that mechanisms would exist in each circuit to maintain its high value irrespective of changes in the hemodynamic conditions.1 In an effort to generate a better mechanical-functional characterization of the arteries, we sought to determiof the position in the systemic arterial circuit.
Differences in the WBF of the different segments studied. Consequently, they offer complementary information to that provided by earlier studies,1,2,9 showing that, independently of the segment studied, the arterial wall displays a similar buffering capacity. This is in agreement with the results of Langewouters et al,22 who, using a complex arterial model, found that the time constant for the arterial wall was similar in segments of the human thoracic and abdominal aorta in vitro. It can, therefore, be postulated that while the viscous and elastic responses are "fixed" according to the "position" of the segment under consideration, to ensure an adequate WBF, the relationship between the two responses is constant. Thus, in segments with the highest rigidity and, therefore, lower systolic reservoir capacity for potential energy, there is a higher capacity to dissipate energy, or higher viscosity, thereby ensuring an adequate WBF.
Clinical Implications
Previous studies have demonstrated that the viscoelastic properties of the arteries vary in different physiological stages (eg, development)10eriosclerosis).7 This study shows that, as for the elastic modulus, while the viscous modulus of a particular segment depends upon its position within the vascular tree, the relationship between them, an indicator of the WBF, remains constant. Changes in the moduli may indicate disease or an adaptive response of the arterial wall to a physiological or pathological state. Therefore, adequate local evaluation of the arteries requires determination of the viscous and elastic responses, of the WBF, and analysis of these parameters according to status of the patient. In addition, given the resemblance of the viscoelastic response between the native artery and the substitute artery used in vascular reconstruction (eg, arterial bypass) is correlated with a lower rate of prosthetic failure,23 knowledge of the mechanical properties of a given arterial segment is fundamental for the selection of a substitute artery.
The study methods and analysis used would allow to simply assess the extent to which different vascular segments are compromised in different disease states, their response to treatment, and their adaptation to different physiological or pathological situations. Thus, systems have recently begun to be used for the local evaluation of arterial function (eg, intravascular ultrasound, echography, and applanation tonometry) that allow continuous in vivo monitoring of the diameter and pressure signal of the arterial "ring" of interest.sing a simple viscoelastic model (Kelvin-Voigt) and methods for the analysis of the instantaneous pressure and diameter in the time domain. Regional differences in these variables were then analyzed. In addition, differences in the pulse wave velocity, the EINC, and the Ep were characterized for the different segments studied. The elastic and viscous moduli increased towards the periphery, showing them to be dependent upon the arterial region. In contrast, the WBF remained constant, independently of the segment analyzed, and was considered to be a property that is independent of the arterial region.
dbia@fmed.edu.uy Daniel Bia.
Departamento de Fisiología. Facultad de Medicina.
General Flores 2125. 11800 Mo