He leído con interés el artículo de Solano-López J et al.1, un importante artículo que halla una asociación estadísticamente significativa (p < 0,05) entre la mortalidad hospitalaria y el diagnóstico positivo de COVID-19 en pacientes con infarto agudo de miocardio mediante la medida de asociación de razón de momios (odds ratio [OR]).

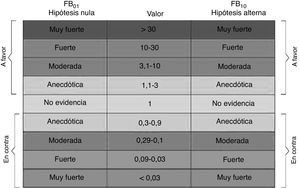
Se recomienda la replicación de las investigaciones clínicas basadas en las pruebas de significación para generar una evidencia con mayor credibilidad en el ámbito de la cardiología. Esto es posible mediante la inferencia bayesiana, pues permite reanalizar el hallazgo significativo reportado por Solano-López et al.1, donde el método del factor de Bayes (FB) se refiere como la probabilidad de los datos bajo una hipótesis en relación con la otra (hipótesis nula frente a hipótesis alternativa)2,3. Es decir, que el factor Bayes estima la cuantificación del grado o evidencia en que los datos respaldan tanto la hipótesis nula como la hipótesis alternativa para su contraste más allá de la interpretación dicotómica del rechazo o la aceptación de la hipótesis nula2,3. La repetición estadística de hallazgos significativos mediante el FB permite reforzar la credibilidad práctica de futuros artículos del área de cardiología (ensayos clínicos, intervenciones y tratamientos, entre otros), que se precisa cuando la inferencia bayesiana produce una evidencia concluyente (fuerte) o superior (FB10 > 10) a partir de la interpretación de clasificación de valores de Jefreys4 para el FB: anecdótica, moderada, fuerte y muy fuerte (figura 1).

Figura 1.

Valores cuantificables del factor Bayes según Jeffreys4.

(0.17MB).

La finalidad de la presente carta es proporcionar un ejemplo sencillo de reanálisis bayesiano para precisar el grado de fuerza probatoria de las hipótesis estadísticas. Por lo tanto, se consideró primeramente la conversión del valor OR (8,23) a tamaño de efecto de correlación (r) mediante la calculadora online de Lenhard y Lenhard5, que arrojó un valor de r = 0,502, y también se consideró el tamaño muestral (187) para la reproducción del FB2. Este método refiere 2 interpretaciones: FB10 (a favor de la hipótesis alternativa de significación) y FB01 (a favor de la hipótesis nula), con un intervalo de credibilidad del 95%6. Los resultados obtenidos del factor Bayes son: FB10 = 3,1810 y FB01 = 3,14–11 y un intervalo de confianza del 95% de 0,383-0,599, lo cual respalda el hallazgo significativo comunicado por Solano-López et al.1 con una evidencia muy fuerte a favor de la hipótesis estadística alternativa (correlación).

Asimismo se estimó el parámetro del factor Bayes máximo (FB10máx = 3,56810) para determinar la estabilidad de los resultados, cuyo valor de mayor magnitud fortalece la estimación de la revaluación bayesiana.

La conversión del tamaño de efecto (TE) y otras medidas estadísticas que se basan en el contraste de hipótesis (d, f, η2, OR, χ2, Z) al coeficiente de correlación (r), de mayor uso universal en las ciencias de la salud, es beneficioso para futuros análisis y reanálisis bayesianos. Además, tales estimaciones son fáciles de realizar mediante la calculadora de Lenhard y Lenhard5. El FB es útil en otras pruebas estadísticas de significación7,8 (regresión lineal, ANOVA, entre otros), cuyas medidas de TE también son convertibles. Se recomienda el manual de Goss-Sampson6 para la inferencia bayesiana de los análisis más utilizados en la investigación de cardiología.

El uso inclusivo de varios TE convertibles afianza el incremento de investigaciones con diversos métodos estadísticos para futuros metanálisis. A su vez, la aplicación del FB es beneficiosa para seleccionar los TE con mayor solidez de evidencia (FB10 > 10) para el diseño metanalítico, ya que refuerza una mayor credibilidad de las conclusiones metanalíticas clínicas.

En conclusión, el FB es un instrumento metodológico de gran utilidad, con una implicación práctica en la toma de decisiones a partir de la confirmación de resultados que sean concluyentes, de mayor relevancia en el contexto de la COVID-19.